Recall that you must choose a set of independent coordinates PRIOR to using Lagrange's equations. One way to verify that your choice of generalized coordinates are independent is to:

• hold all but one of the generalized coordinates fixed
• determine if the remaining generalized coordinate can be changed without violating any of the constraints of the system.
• repeat this procedure for all N generalized coordinates.

Here we will demonstrate this number of DOF check on the following example from the lecture notes. Here we will use the three generalized coordinates shown.

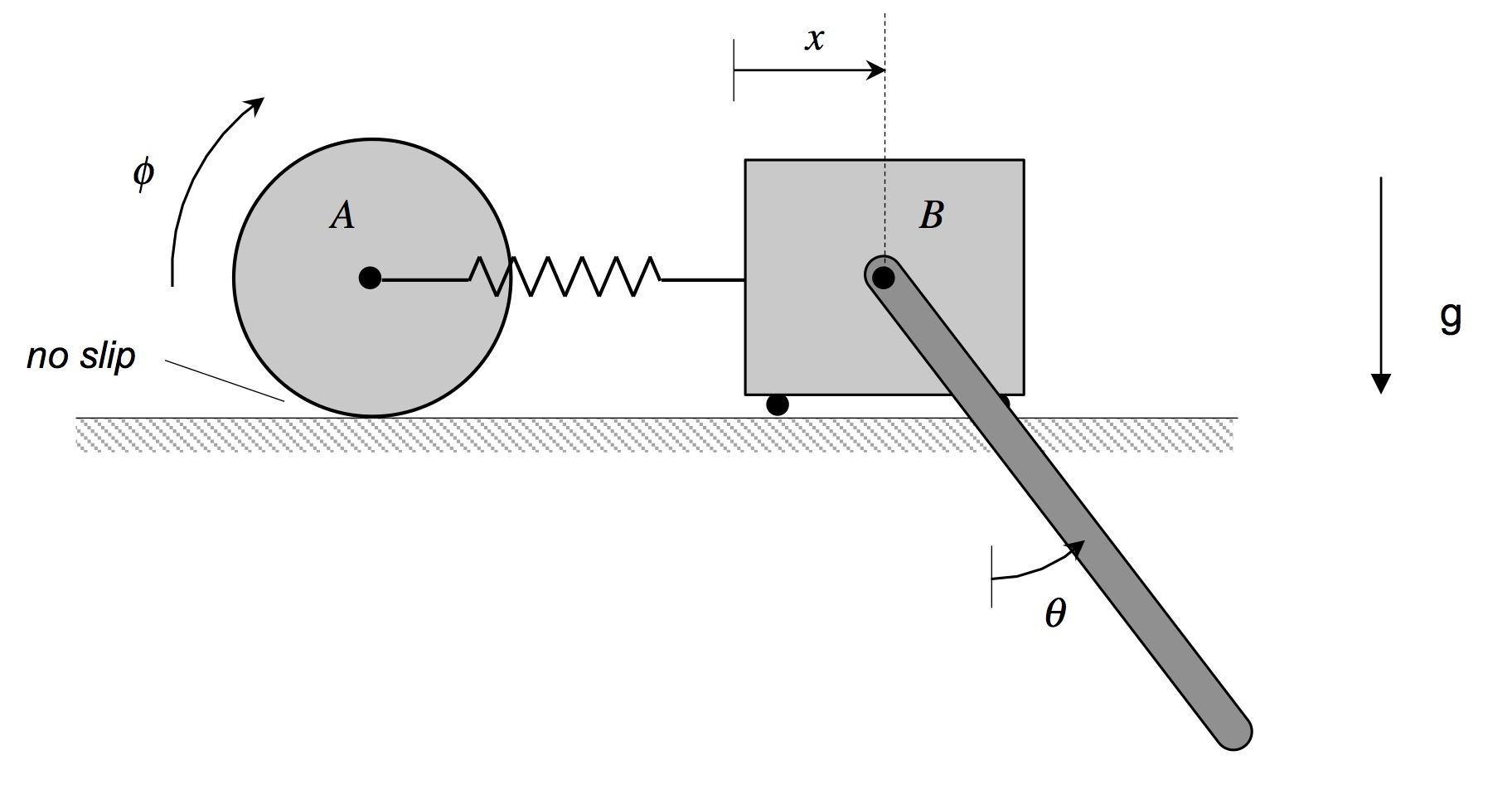
Shown below are animations of this check. As you see, it is possible to hold any two of the coordinates fixed and still be able to change the remaining coordinate. Therefore, the system is verified to have three DOF's.

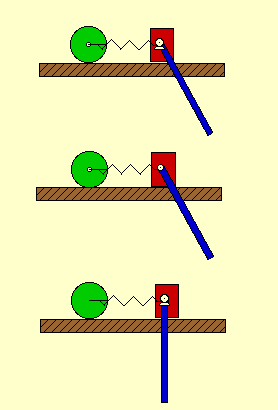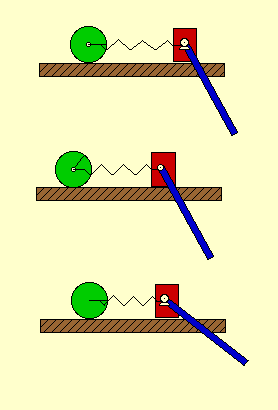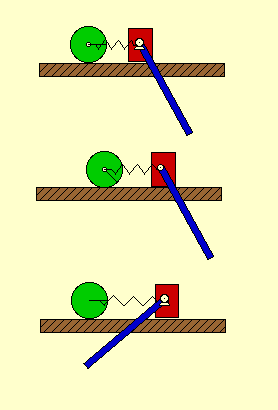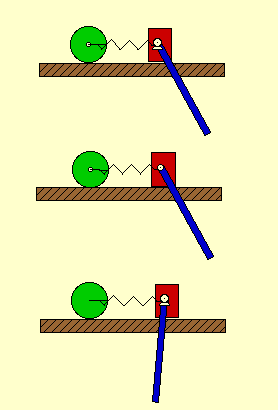Hold the rotation of the wheel and bar fixed. You can still move the block. Hold the block fixed and the rotation of the bar fixed. You can still rotate the wheel Hold the wheel and block fixed. You can still rotate the bar.