| Problem statement Solution video |
DISCUSSION THREAD
Discussion
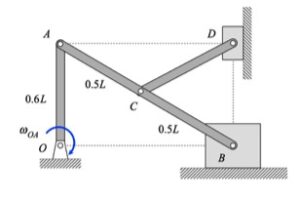
The animation above shows the motion of the mechanism over a range of input angles of link OA. For a given position, envision the location of the instant centers (ICs) for links AB and CD. Do the directions and magnitudes for the velocities of points B, C and D agree with the location of these ICs?
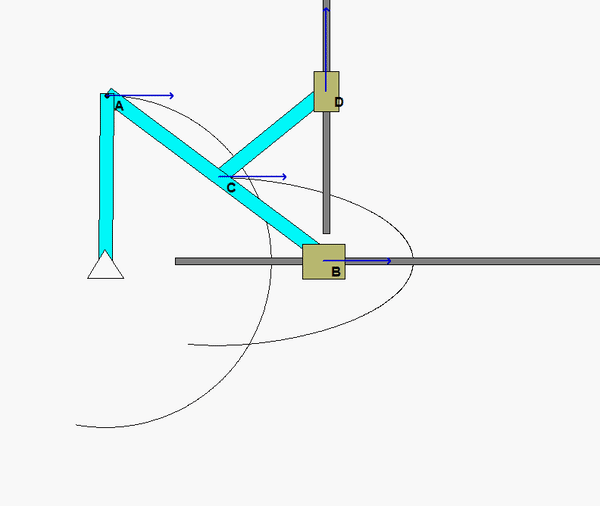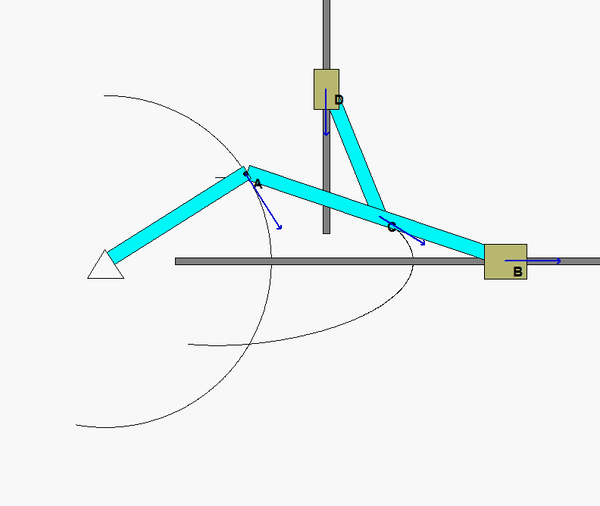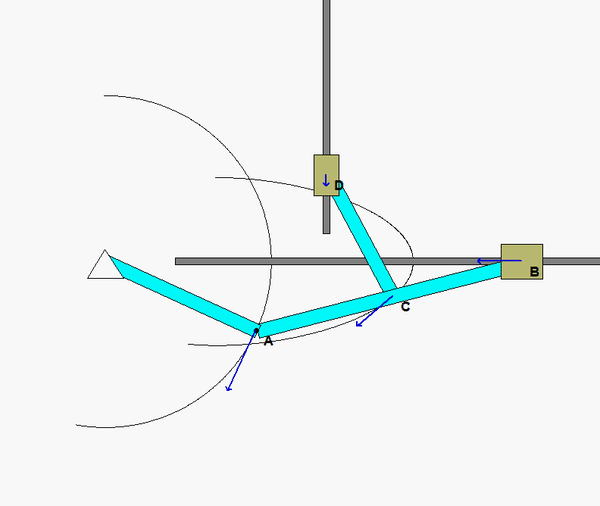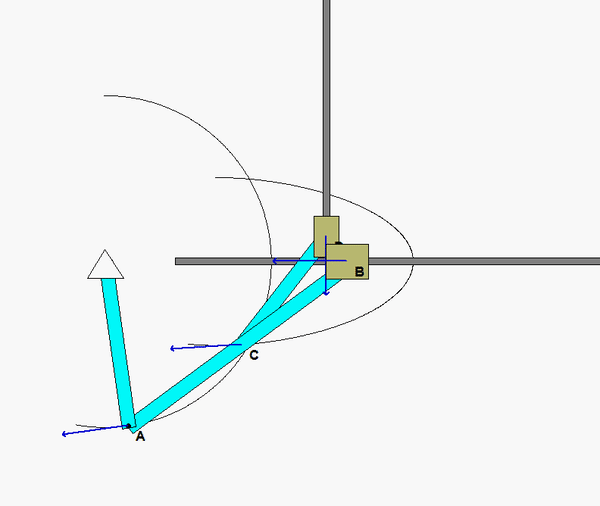
Shown below is a freeze-frame of the mechanism motion at the position for which you are asked to do analysis. From this figure, where are the two ICs for links CD and BC? In particular, how does the position of the IC for AB relate to the relative sizes of the speeds of points A, C and B? What is the angular velocity of link AB at this position?

Any questions?? Please ask/answer questions regarding this homework problem through the "Leave a Comment" link above.
If two points on a rigid body have parallel velocity vectors with different magnitudes but their tails don't have the same normal line, does that rigid body still have a center of instantaneous rotation? Is such a thing even possible with a rigid body?
As discussed in class, if the perpendiculars of the velocities of two points on a rigid body are parallel but not coincidental, then the body is in pure translational - no rotation. If the parallel lines are coincident, the IC lies along that line.
Oops, I just realized that this is the wrong question. I don't know how to delete posts, so I'll just copy my post onto the right one.
Does this also mean that the translational velocities of points on the rigid body are also zero? so Vc and Vb are zero?
According to this website, it would be the same velocity everywhere on AB. I.e. Va = Vb= Vc, but does not mean that Vb and Vc are 0.
Website: https://emweb.unl.edu/NEGAHBAN/EM373/note16/note.htm#:~:text=The%20lines%20are%20parallel%20(they,points%20must%20be%20the%20same.
Assuming that there is no translational velocity, it seems that it would be 0.
No, it just means that the velocity for ALL points on the translating body are EQUAL (but not zero).
What should our answers be in terms of? Since there are no "given" variables other than Woa, should everything be in terms of Woa and L?
Yes, the given variables are omega_OA and L.
Can we give a written explanation, or do we need to show visuals for each step in the solution?
Simply showing the construction lines and writing down the conclusions will suffice.
Can we use the velocity equations to solve for v_A just without the vectoral components, as in just using the magnitudes v_A = omega_OA*r_A/O?