| Problem statement Solution video |
DISCUSSION THREAD
Any questions??
As P moves around on the circular track, two things occur:
- The normal force N on P due to the circular guide is proportional to the centripetal acceleration of P: N = mv2/R.
- A friction force opposes its motion, where the sliding friction force is proportional to the normal force between the circular guide and P: f = μkN = mμkv2/R.
From this, we see that the friction force goes to zero as the speed goes to zero. What does this imply about P coming to rest? Can you see this in the animation of the motion below?
HINTS:
You will need to use the chain rule of differentiation to set up this problem: dv/dt = (dv/ds)(ds/dt) = v (dv/ds).
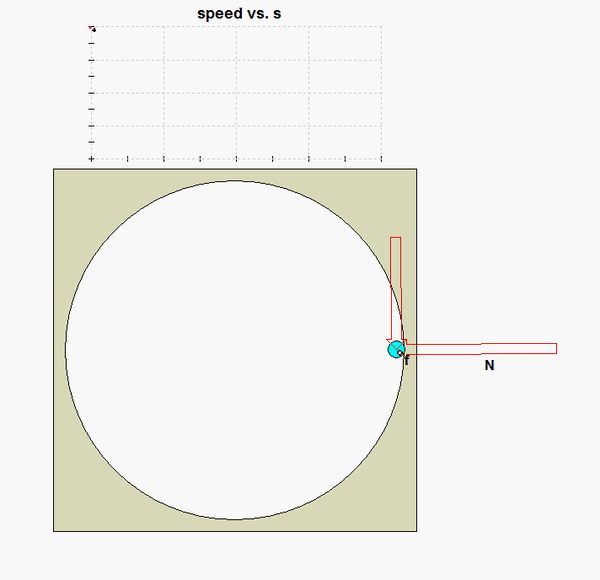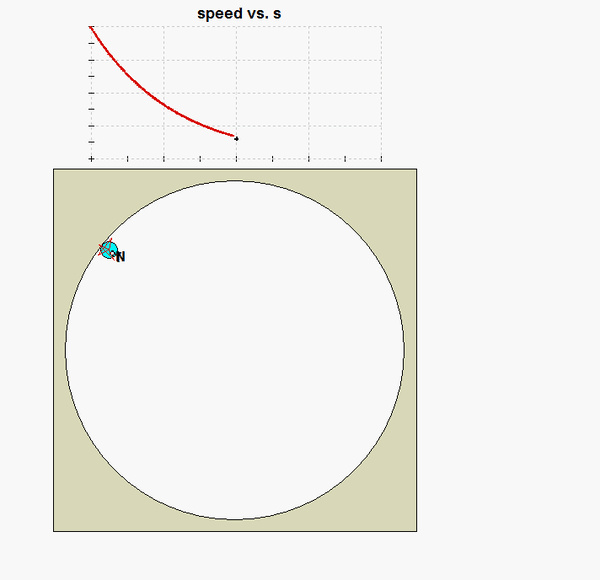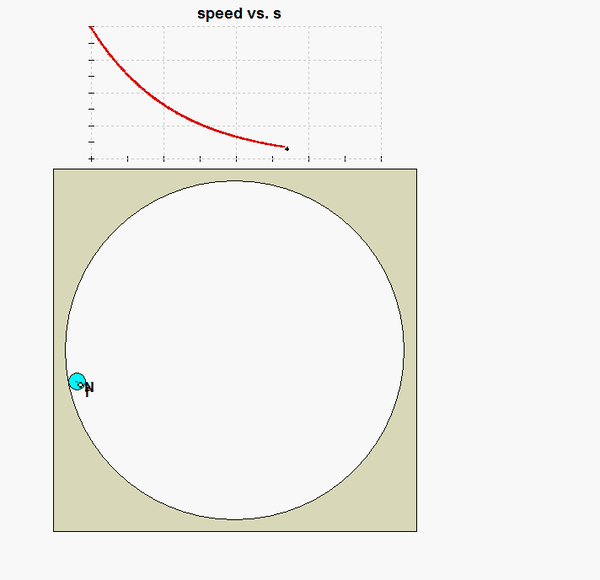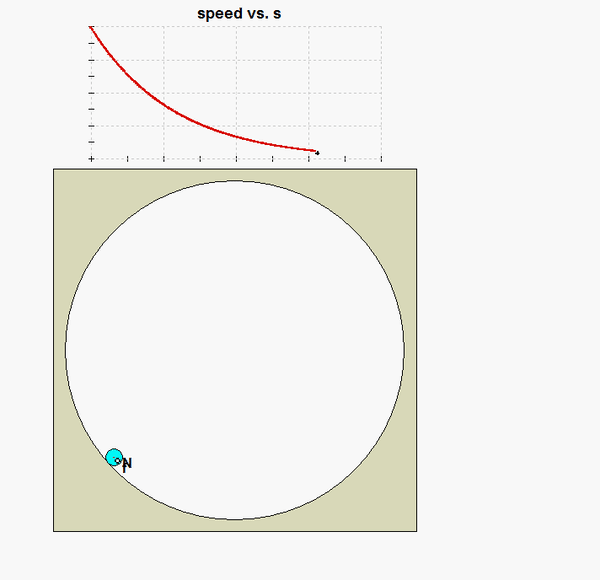
I got an asymptomatic solution for C, and the animation seems to concur. So technically speaking, would the ball ever come to rest?
Let's hear from some more people on this.
I got that as well. I decided that since using e^-5 is 0.0067, that is a close enough approximation for zero. However, I wasn't sure if just declaring a time closest to zero and then solving is correct since it should technically go to infinity.
I got the same problem. What I did is used e^-3, which is 0.0498, and that can be considered as no speed. You can also use -4, -5, and down, but that would not significantly change the distance traveled.
i am also getting an exponential decay function, which never technically touches zero. as s goes to infinity, i would never touch the x axis signifying that the velocity is equal to zero.