| Problem statement Solution video |
DISCUSSION THREAD
Discussion and hints:
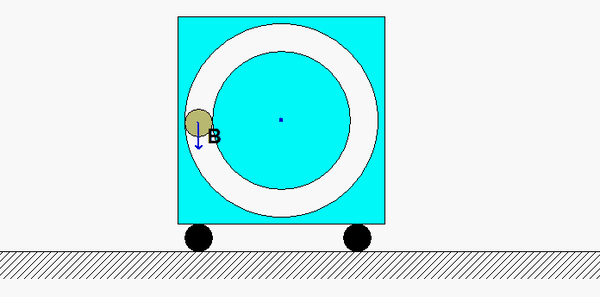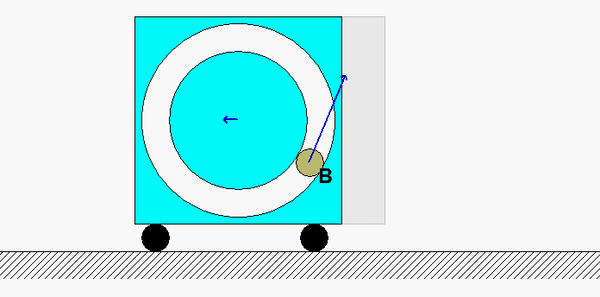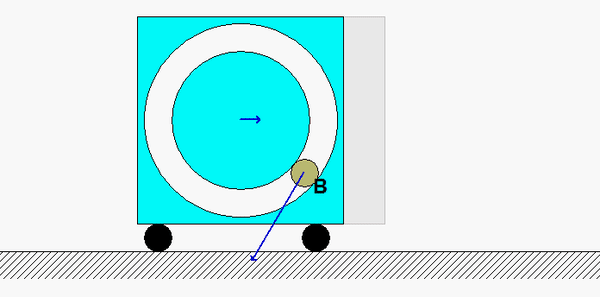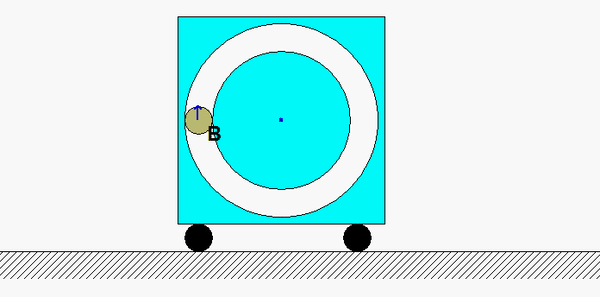
Recall the following four-step plan outline in the lecture book and discussed in lecture:
Step 1: FBD
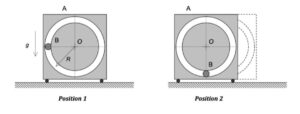
Draw a free body diagram of the system made up of A+B.
Step 2: Kinetics (linear impulse/momentum and work/energy)
From your FBD above, what is the external force acting on the system of A+B in the horizontal direction? What does this say about the linear momentum of this system in that direction? Also, are there any non-conservative forces acting on the system of A+B? What does this say about the mechanical energy of the system?
Step 3: Kinematics
At position 2, B is moving only in the horizontal direction. There is no vertical component of velocity of B at position 2.
Step 4: Solve
Solve for the speeds of A and B from the above equations.
Any questions?
To find the velocity of A using the impulse equation, would A's mass be M or (m+M)
The answer to this depends on your choice of FBD.
* If you choose your system as A alone, then your momentum equation will just include A: M*vA.
* If you choose your systems as A + B, then your momentum equation will include both A and B; that is you will have the sum of the two terms M*vA + m*vB_x.
The second option above is recommended.
For part B, should we represent work due to the normal force as non-conservative or as a form of potential energy?
The normal force does not have a potential of which we are aware. Therefore, if that is the route you take, you would need to calculate the work through integration.
Note, however, that if you consider block A as your system, the work done on A is equal to the change in KE for A alone. Since you know the initial and final speeds of A, you can readily find the change in kinetic energy directly from that information.
Make sense?
Yes, I just didn't know how we should write it when showing our work.
Does this mean we can use integrate the force over time and use the change in momentum like we have done in past problems?
Never mind, I figured it out.
Even easier than that.
For Part a), use conservation of linear momentum and conservation of energy to find the velocities of A and B. No integration needed.
For Part b), find the change in kinetic energy of A. No integration needed. This will give you the work done on A (as described above).
Does that help?
When solving part A I used the LIM equation and got the VA2 in terms of VB2. Then I used a work energy equation with respect to B to solve for the velocity of B at position 2. In that equation I only had T2 and V1 terms after placing my datum at B in position 2. Would this be an accurate approach to the question?
I would need to see your work to say for sure; however, what you describe here is the correct approach for solving the problem.
For part A, I used the LIM equation to find the velocity of A in terms of the velocity of B at position 2. After this, though, I'm not sure whether to use the work-energy equation for just particle B, or for the system of A and B. Both situations seem like they should have the same nonconservative work of zero, but they give different answers. Should I use the work-energy equation for just particle B or for the system as a whole?
You need to use the kinetic energy equation with the velocity and mass of A.