| Problem statement Solution video |
DISCUSSION THREAD
Discussion and hints:
Recall the following four-step plan outline in the lecture book and discussed in lecture:
Step 1: FBDs
Draw individual free body diagrams for the bar and the disk.
Step 2: Kinetics (Newton/Euler)
Write down the Newton/Euler equations for the disk and for the bar based on your FBDs above.
Step 3: Kinematics
You need to use the rigid body acceleration equations to relate the accelerations of O and the center of mass of the bar, G, through the angular acceleration of the bar. Also, you need to relate the acceleration of O to the angular acceleration of the disk.
Step 4: Solve
Solve your equations for the angular accelerations of the bar and the disk.
Any questions?
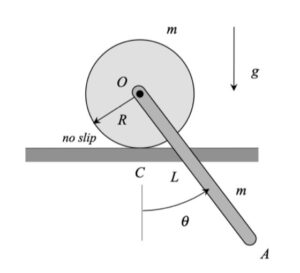
Am I correct in assuming the bar isn't rigidly fixed to the disk? it doesn't look like it in the figure but the problem is unclear on it.
The problem statement says that the bar is "pinned" to the disk. As we have used throughout the semester, a pin joint can transfer a force from one body to another; however, the pin joint is not a connection that can transmit a couple (that is, the two bodies can rotate relative to each other).
Can we count force OA as one force? Or do we have to split it into X and Y components that are not necessarily related
I was able to solve for the angular acceleration of the bar from just one equation (the moment of the bar about point O) since the only moment about this point is gravity and all other values are known. This feels suspiciously simple so is there some other relationship I am missing?
I originally got that as well but I realized you can't take the moment about O because it is a pin joint. Rather I took a moment about the center of that bar at point G.
For the disk, you can take a moment about point O, since O is the center of mass of the disk.
For the bar, you cannot take a moment about O because O is neither a fixed point nor the center of mass.
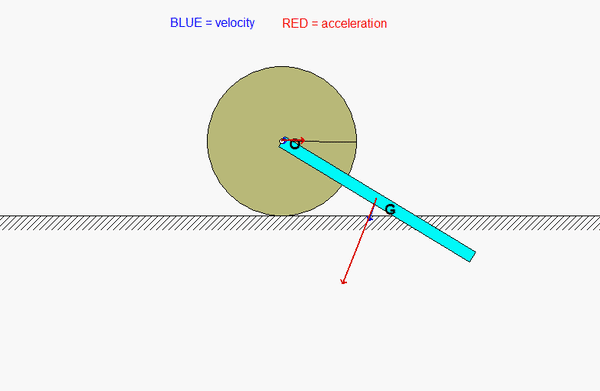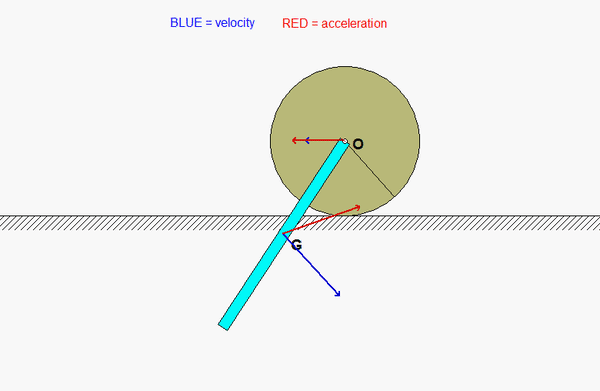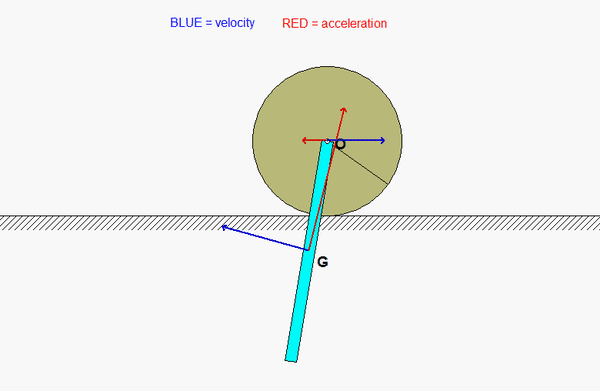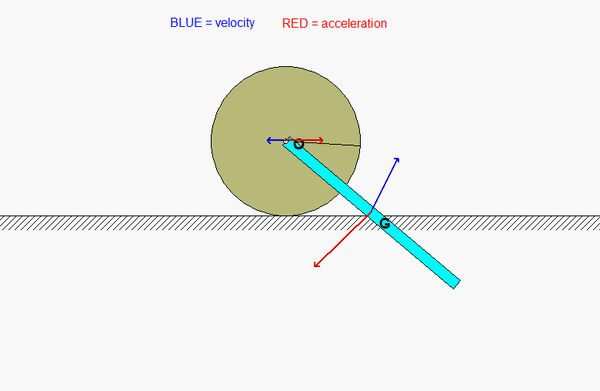
Can someone explain why the animation velocity and acceleration looks the way that it is? it is not intuitive to me, especially the velocity and acceleration of the center of the bar.
Note that the velocity of point O is always horizontal since O moves along a horizontal straight path.
The velocity of G is more complicated. There you would write down:
v_G = v_O + omega_bar x r_G/O
That is more difficult to visualize.
Same thing for acceleration. The acceleration of O is always horizontal since O travels on a straight horizontal path. For G:
a_G = a_O + alpha_bar x r_G/O - omega_bar^2 *r_G/O
Even more complicated that v_G.
After following the steps laid out, I arrived at two equations, two unknowns - angular acceleration of the disk and bar, with equations derived from kinetics and newton euler. don’t forget the parallel axis theorem!
I had a bit of trouble putting together the right equations with one another to solve for the angular accelerations. Is there an easier way to go about the "Solving" aspect of the problem (a methodology to follow when you have numerous unknowns and equations)?