Chapter 6 Homework

Homework H6.I - Fa24

10 Comments
Problem statement
Solution video

DISCUSSION THREAD

Ask your questions here. Or, answer questions of others here. Either way, you can learn.

DISCUSSION and HINTS

The particular solution for the equation of motion for this system is shown below for two values of the frequency of excitation, ω. As we have seen in lecture, and as shown below, when the excitation frequency is less than the natural frequency,ωn, the response is in phase with the excitation, and when the frequency is greater than ωn, the response is 180° out of phase with the excitation. Can you see this in the animations below?

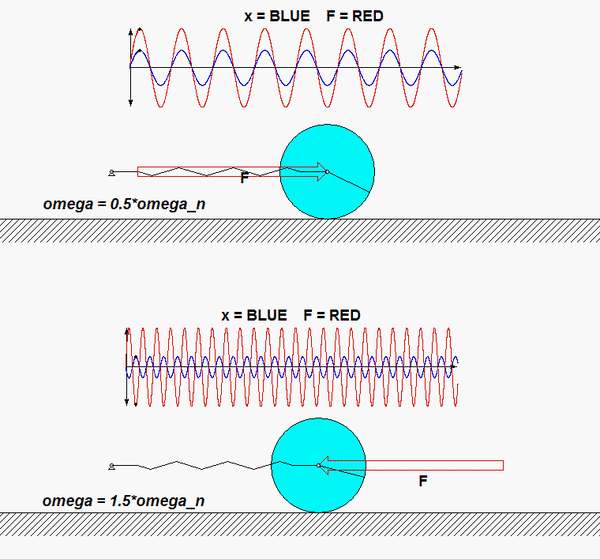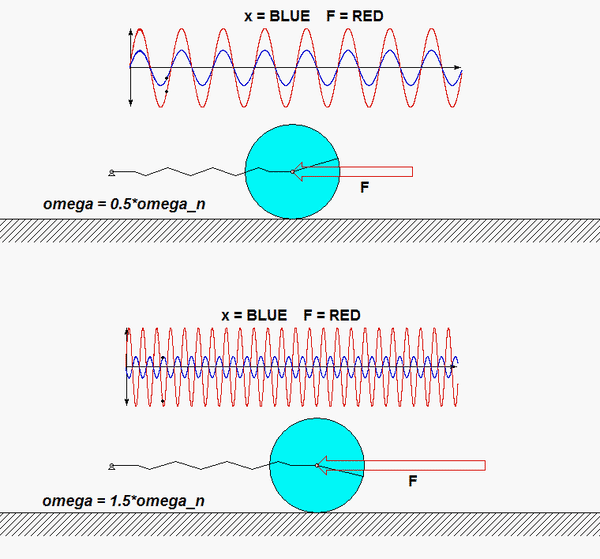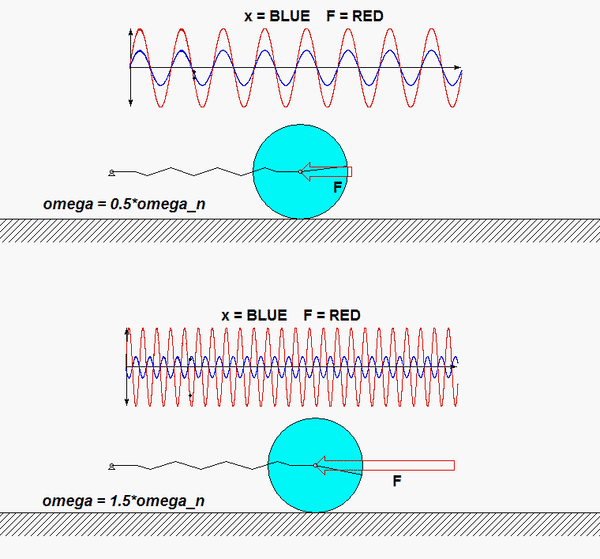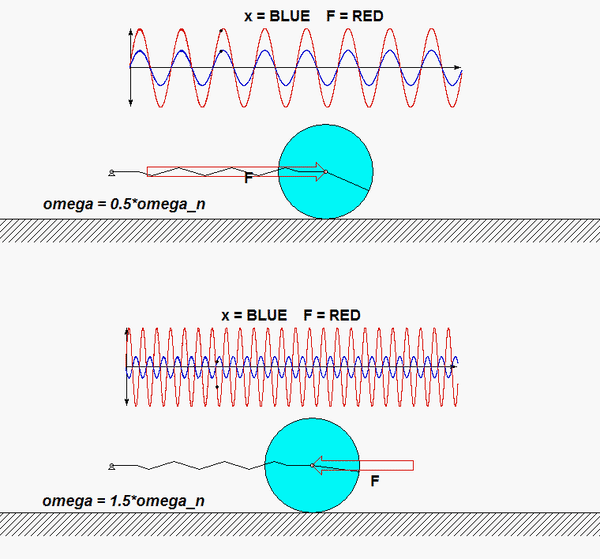
Recall the following four-step plan outline in the lecture book and discussed in lecture:

Step 1: FBDs
Draw a free body diagram (FBD) of the disk. It is important to temporarily define a translation coordinate that describes the position of the center of the disk, O. Let's call that variable x, and have it defined as being positive to the right.

Step 2: Kinetics (Newton/Euler)
Use Euler's equation about the no-slip contact point C.

Step 3: Kinematics
Relate x_ddot to θ_ddot through kinematics.

Step 4: EOM
Combine your equations from Steps 2 and 3 to arrive at your EOM in terms of θ.

Once you have determined the EOM for the system, identify the natural frequency from the EOM. From the EOM we know that the particular solution of the EOM is given by: xP(t) = A*sin(ωt)+ B*sin(ωt). How do you find the forced response coefficients A and B?

Does your result here agree with the expected relationship between excitation frequency and response with regard to the "phase" of the solution?

10 thoughts on “Homework H6.I - Fa24”

  1. I'm a little confused with the in or out of phase terminology. Does in phase mean the applied force and spring force are acting in the same direction? And for out of phase, they act in opposing directions?

    1. In Phase: When two quantities are in phase, they hit their maximum, minimum, and zero points at the same time. For forces, this means the applied force and the spring force change together, but they don’t necessarily act in the same direction. For instance:
      - If the applied force and the spring force are both acting in the same direction and oscillating together, they’re in phase.
      - If they’re always acting in opposite directions but their magnitudes still sync up, they can also be considered in phase, depending on how you define it.

      Out of Phase: When two quantities are out of phase, their oscillations don’t line up. Specifically:
      - If they’re 180 degrees out of phase, they reach opposite extremes at the same time (e.g., one is at its maximum while the other is at its minimum). This usually means they’re acting in opposite directions.
      - If they’re out of phase by some other angle (not 0 or 180 degrees), there’s an offset in their timing based on that angle.

      This is my understanding of the concept and I could be mistaken but i do hope this clears it up for you!

      1

    1. Maybe. It depends on how you define "x". Since C is the IC for the disk, I agree that the speed of O is the angular speed of the disk times R.
      * If you have defined x to be positive to the right, then x_dt = +R*theta_dot.
      * If you have defined x to be positive to the left, then x_dot = -R*theta_dot.

      The sign on that term is very important. If you get that sign wrong, your coefficients in the EOM will be wrong, not just their signs.

    1. Not really. It is one option out of two.

      The direction chosen is not relevant to solving. What is relevant is ensuring that you make your translational coordinate x to be correctly related to the rotational coordinate in Step 3 Kinematics, and that you use the same sign conventions for displacements/rotations as you do for forces/moments in Step 2 Kinetics.

Leave a Reply