Chapter 1 Homework

Homework H1.C - Sp 25

17 Comments
Problem statement
Solution video

DISCUSSION THREAD

Ask and answer questions here. You learn both ways.

DISCUSSION and HINTS

As expected, the acceleration of P has both non-zero tangential and normal components.

  • From the equation provided for speed as a function of distance traveled, the speed of P is monotonically decreasing over the range of motion shown in the animation below. Therefore, the tangential component of acceleration always points "backward" of the direction of motion.
  • The normal component decreases as P moves along the track since the speed of P is decreasing.

Can you see these two things in the animation below?

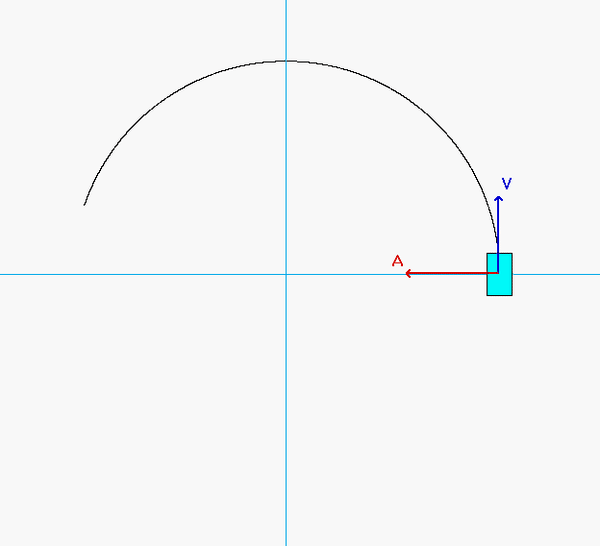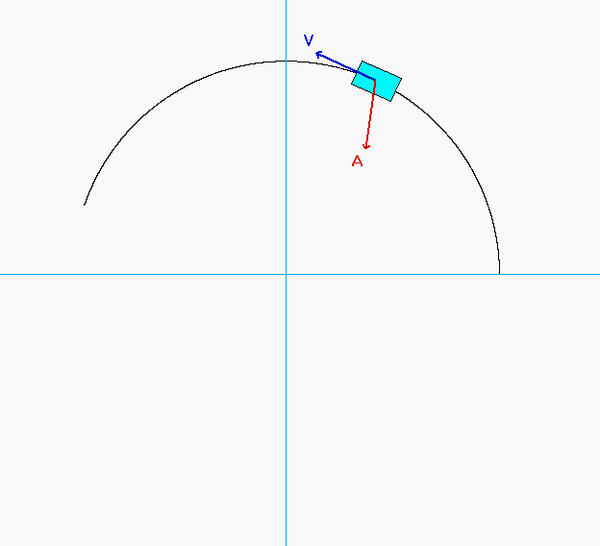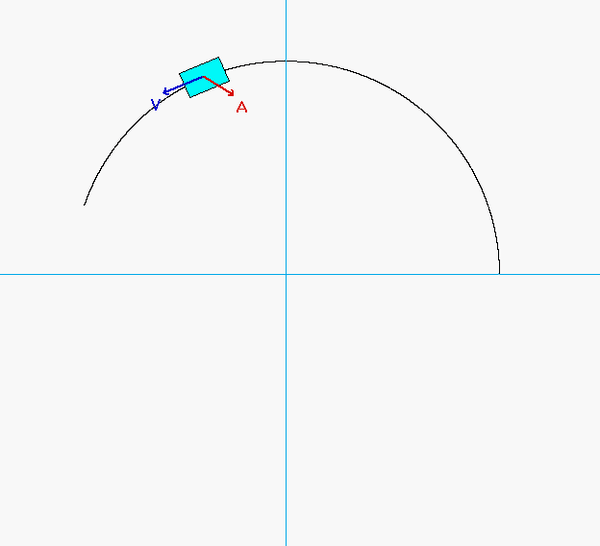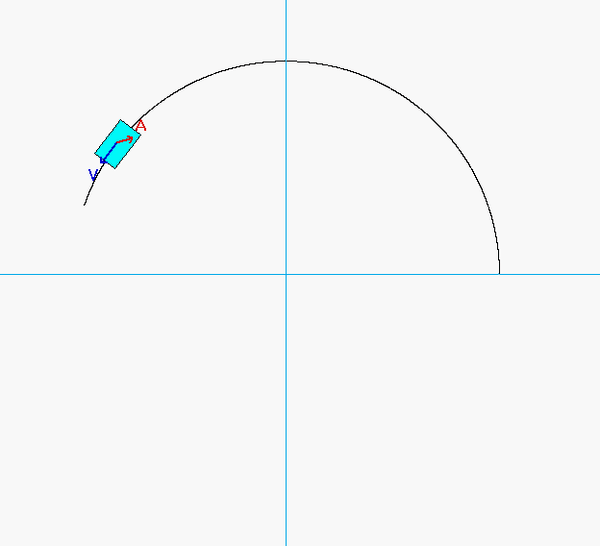
Recall that the general path description velocity and acceleration equations are given by the following:

v = v*et
a = v_dot*et + (v2/ρ)*en

17 thoughts on “Homework H1.C - Sp 25”

    1. Yes! This is because the rate of change of speed (the tangential component) is just what change of speed the driver would see on the speedometer. The change of speed on the speedometer does not account for the total magnitude of acceleration, as it does not include the centripetal (normal) force, which also changes as a function of speed

      1

  2. Slightly silly question. When we plug in our value for S to find V and V_dot should we be in radians or degrees?

  3. Not a silly question.

    Note that b*s = (1/m)*(m) = dimensionless. Therefore, the trig functions of b*s (such as cos(b*s)) are expecting an argument in RADIANS.

    Make sense?

  4. I found the acceleration in the form (___ et + ___ en ). I'm confused how to find the magnitude of acceleration from here. Can I treat the et and en like i and j in a vector?

    1. I believe you can find the magnitude the same as if it were i and j but you don't need to do any conversion. This comes from the fact that the magnitude equation is just pythagorean theorem, and the full vector is the hypotenuse (length is the magnitude) of the triangle which sides are the et and en components

      3

      2. I did the same thing to find the magnitude of the acceleration and I don't know how else we would calculate this.

  6. The speed is given to us in terms of the distance traveled, s. Importantly, it is NOT given to us in terms of time. In order to take the derivative of v with respect to time, we need to use the chain rule:

    dv/dt = (dv/ds)*(ds/dt) = v*(dv/ds)

    So, the answer is yes.

    1. While solving the equations, do you need to write out your units through each step or can you insert them at the end? Will they take off credit?

      1. I would write out the units at the beginning to show that you understand what units are being used. Then insert them at the end of the problem to show you understand the value you were calculating.

      2. It is best to leave your answer in symbolic terms until the last step. Put in the numbers with units. This will help you find errors in your analysis if the units do not work out correctly.

        1. What I like to do with units is write them at least once when I initially write the numbers into the equations to make sure I'm not losing my mind. If the unit's are pretty straightforward I might drop them until my final answer but if I'm in doubt I'll always write them down to make sure I'm not being a silly goose.

  7. Basically the same as example 1.A.3 except you're solving for tangential acceleration at point B. You can do this by derivating the velocity function then plugging in the numbers they gave.

Comments are closed.