| Problem statement Solution video |
DISCUSSION THREAD

Ask or answer questions here. Either way, you learn.
DISCUSSION and HINTS
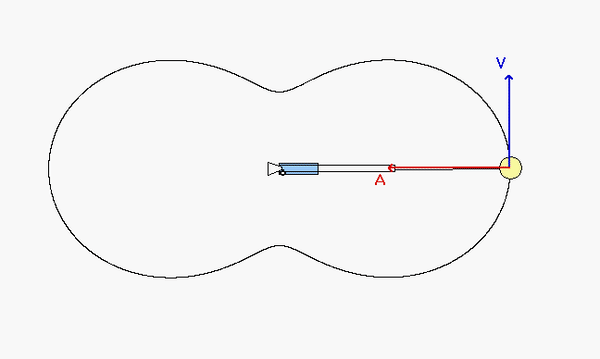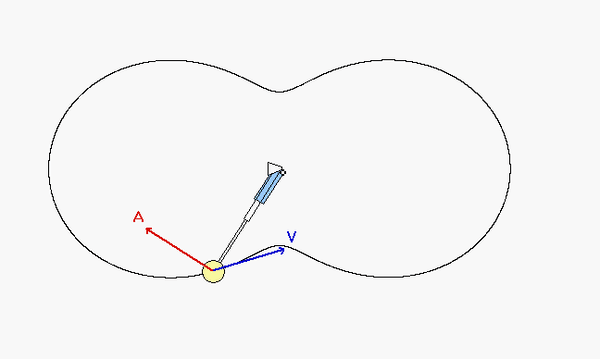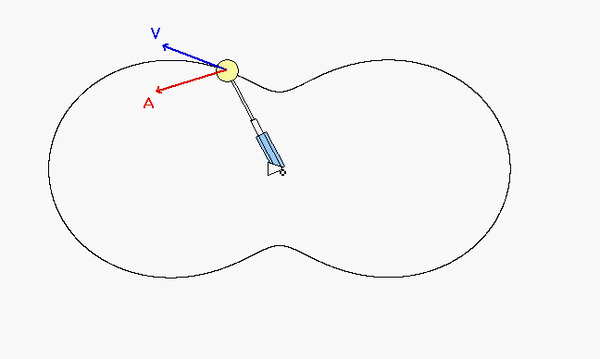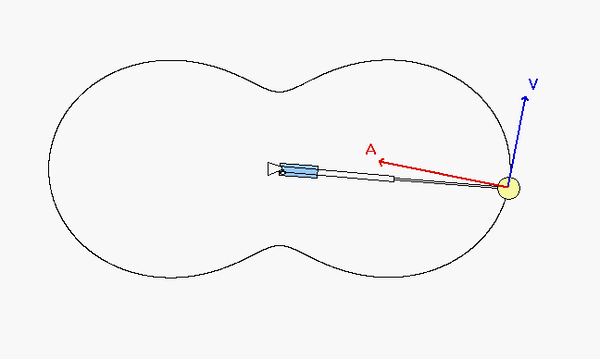
The motion of P is shown in the animation below. As we saw in our last lecture, the velocity of a point is always tangent to the path of that point. The acceleration of a point will always have a normal component that points inward on the path. Can you make these general observations in the motion of P shown below? Can you tell from the animation when P is increasing in speed and when P is decreasing in speed? (Look at the direction of the tangential component of the acceleration relative to the direction of the velocity.)
Note that in this problem we are not given the radial variable r as an explicit function of time. Because of this, when we are finding dr/dt when need to use the chain rule of differentiation; that is, we should use: dr/dt = (dr/dθ)*(dθ/dt).
What should the units be in? m/s or rad/s
A good way to remember what units should be is to remember that r' is the equation for velocity and velocity is usually measured in m/s r'' is acceleration which is usually in m/s^2
r is in meters.
dr/dt is in m/s.
d^2r/dt^2 is in m/s^2.
I understand the units should be in m/s, I am just confused on how to get there. For example in the e-theta term of velocity you have r times theta dot which is meters times rad/s. How do you get to m/s from that product?
Radians are a unitless quantity. rad-m/s is equal to m/s.
Keep in mind that radians is a dimensionless measure of an angle. Therefore, m*rad/s is the same as m/s.
I am confused as to why "θ = π rad" is given as a parameter, because θ is a variable. Does this mean they want us to find the velocity and acceleration at θ = π rad specifically and not in general?
Yeah, I'm pretty sure they want you to find velocity and acceleration at theta = pi rad specifically. This is exactly like Example 1.A.4 that we did in class on Friday.
For this problem, find velocity and acceleration in terms of the position variable theta. At the end, substitute in theta = pi since we want to know velocity and acceleration that that value of theta.
When you do the derivative of smth like sin(2x) is it cos(2x)*2x' with the chain rule?
If you mean cos(2x)*(2x)' then yes, the chain rule says that you have to multiply by the derivative of the function inside.
Yes, that is correct.
If θ' is considered angular speed and θ'' is angular acceleration, how would r' and r'' be considered (in words, not units)? Is it the same thing?
There are no special names, other than the time derivatives of r.
For the second derivative in finding the acceleration, since θ' is a constant, it would just be squared when taking the derivative according to the chain rule again right?
Not sure of what you are asking. Since theta_dot = constant, then theta_ddot = 0. This leaves only one of the two terms of the e_theta components for acceleration to be non-zero
That was what I found. When you find the second derivative, you have the "leftover" theta dot from the original term. So, you would just multiply them and have a thetadot squared term.
Where can I access TA office hours schedule/ times?
You can view the TA office hours scheduling by going to "Daily Schedule - SP 2025" --> "Course Quicklinks" --> "Tutorial Room Schedule"
Do we have to do product rule for r double dot.
I did not do the product rule. I just treated theta dot as a constant for the purposes of the derivative.
You should be using product rule, keep in mind that when doing this there is a chain rule involved so you will end up with a term that has theta_dot^2
Yes, I believe that we follow the chain rule and product rule systematically. After you find r_dot, you should have a sin(2theta) and a theta_dot value. When we differentiate r_dot, we need to compute the derivative of both.
In the animation, when the particle reaches the bump between the two circles, why does the direction of acceleration change to facing out of the circles, when in the discussion section it states that acceleration will typically point inward?
I like to see it as the bump being part of another circle technically, and it points towards the center of that circle. Therefore leading to the difference in direction of acceleration vector. That’s just how I see it.
Good observation.
The theory says that the normal component of acceleration always points INWARD to the path. Here "inward" means toward the center of curvature. The center of curvature is the center of the circle that fits the path in terms of slope and curvature.
At the two "bumps" that you mention, the normal component of acceleration still points "inward" to the path since in those regions of the path the center of curvature is outside of the closed loop of the path.
If I make my e^r direction outward from the vector r, and acceleration points inward towards the center of rotation, would that mean my acceleration value should be negative?
I started this question with finding r dot, and input r dot into velocity equation in polar unit vector form. Next I found r double dot, which is derivative of r dot. Finally I input the r double dot on acceleration equation. I was confused about how rad/s changes to m/s but I read the comments and I understood.
I started by finding r dot, r double dot, and theta dot. We know theta double dot is zero because it is given that theta dot is a constant. From there, I plugged in the given values and results I just calculated into the polar velocity and acceleration equations for my answer. I was confused about the units, but the other comments helped me understand how they are in m, not rad.