| Problem statement Solution video https://youtu.be/_9fXrFRcR-w |
DISCUSSION THREAD

We encourage you to interact with your colleagues here on conversations about this homework problem.
With the polar description, we write the velocity and acceleration vectors for a point in terms of the polar unit vectors er and eθ. These two unit vectors are shown in magenta in the animated GIF below.
- er points outward from the observer O toward point P
- eθ is perpendicular to er and points in the positive θ direction.
The velocity (in blue) is seen to be tangent to the path, as expected, The acceleration (in red) has both tangential and normal components: the normal component always points inward on the path, and the size and sign of the tangential component is directly tied to the rate of change of speed of P, also as expected.
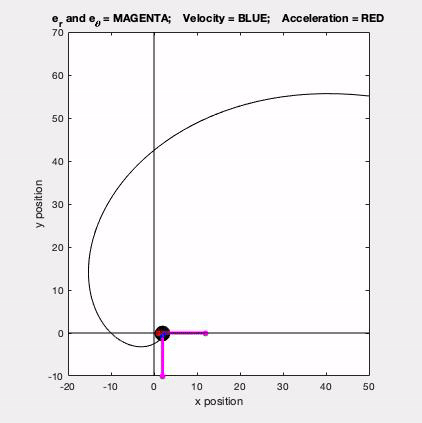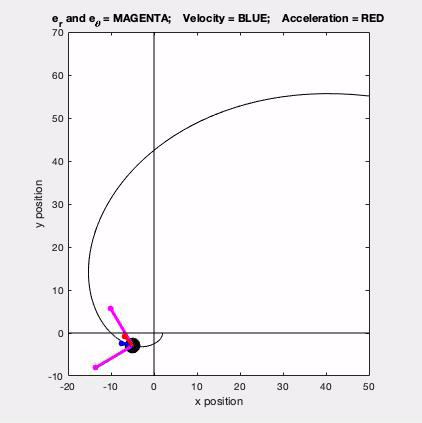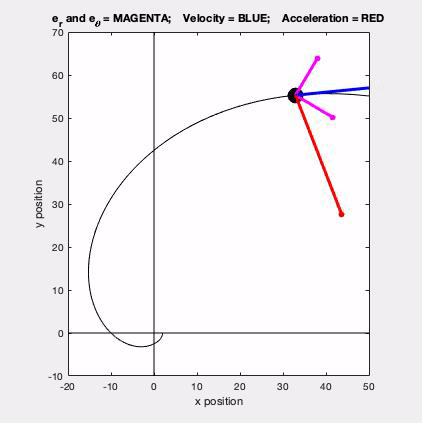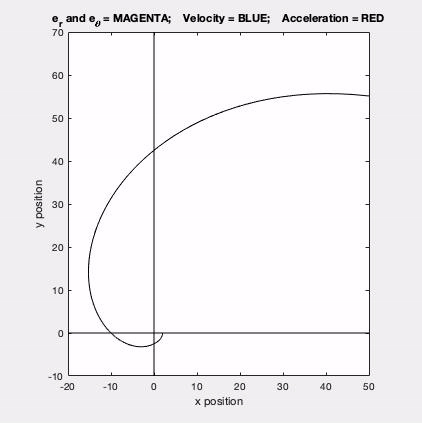
In terms of problem solving, this problem is straight forward. Both r and θ are given as functions of time. The components of the velocity and acceleration vectors are found directly from the differentiation of r and theta with respect to time. The chain rule of differentiation is NOT needed here.
Some additional observations:
- Although r_ddot = constant, the r-component of acceleration is NOT constant.
- Although θ_ddot = 0, the θ-component of acceleration is NOT zero.
I am having issues with the units for r_dot because I am getting 2/s for the e_r component of the velocity equation. I need the units to be in m/s. help
Olivia:
The value for the parameter "b" should be: b = 0.5*(m/s^2). We will correct that in the problem statement. Thanks for bringing this to our attention.
I am probably making a simple error here, but in part b of the assignment, I plugged the value of theta (pi) into the equations for e(r) and e(theta) given on page 38 of the lecture book and did not get the directions that I anticipated based on my sketch. I got that e(r)= -j and e(theta)= -i. Why is this? Should I use these or the directions based on the sketch, which if I am correct would be e(r)= -i and e(theta)= j?
Hi Monet!
I believe your first assumption is correct and you did not make an error. I ran into the same thing. The example on Page 38 of the lecture book is different than this problem because the vectors are pointed in a different orientation. But if you find the derivative of e(r) and e(theta) the proof and formula on the rest of the page 38 is true and lines up with the rest of this problem.
As Ella says above, there are a number of ways to define the polar angle theta. It could be defined CW or CCW. It can be measured from any number of reference lines on the page. As Ella also says, the fundamental equations for velocity and acceleration still apply for any choice of this angle. You simply need to draw the directions of the polar unit vectors based on the definition of theta that is used.
So on page 38 since theta is defined between the y-axis and e(r), and in this problem it is defined as between x-axis and e(r), we can use the same formulas except define a new angle phi that is 90 - theta? And use that? Or would that be incorrect?
My recommendation is to keep things simple. For Part b), just use trig.Write e_r in terms of i and j. write e_theta in terms of i and j. Substitute these into your velocity and acceleration results from Part b). That's it.
I am confused about how to find theta for part b. Any suggestions on where to start that?
There is an equation in the given statement that has the angle theta as a function of time. You just need to solve the equation for t=2s and you have your angle
Hi! The way I solved for theta was plugging t = 2s into the given equation of theta(t) = ct. Hope this helps!
The equation for theta as a function of time is given. You would start by plugging in and solving for theta at 2s.
To find the angle theta between er and the positive x-axis can be found by solving the theta function at t=2 seconds. But keep in mind this is not the angle between the etheta and the x-axis. You can find that angle by using (pi/2)-(theta) which you can use for finding its projection.
When working on converting the velocity and acceleration in terms of e^r and e^theda to cartesian coordinates, are the i and j vectors always drawn in the positive directions. As I am trying to form triangles with e^r and e^theda with those unit vectors.
Yes, i_hat points in the positive x direction, and j_hat points in the positive j direction.
I am having some confusion converting the e^r and e^theta into i and j vectors. Do you begin by drawing the j down from p and then the I, or vis versa?
As mentioned above, i_hat points in the positive x direction, and j_hat points in the positive j direction.
As CMK said, i points in the positive x direction and j points in the positive y direction. I think that is super helpful when doing the substitution equations for e^r and e^theta to remember, and then you can use it to check your answers and the signs.
I am confused as to the direction of rotation in this problem. I understand that it is moving clockwise; but why? The function theta(t) does not have a negative sign, which in my understanding of this, would be the reason it rotates clockwise. Just curious if there is an intuitive explanation to this, or if we are just supposed to look at the picture and see the direction of rotation. Thanks!
The diagram in the problem statement basically defines that theta increases in the clockwise direction. Normally with polar coordinates you measure theta off of the x axis going in CCW direction but this problem does it this way. In an example in the lecture book they measure off the y axis so it really just depends on how the problem defines theta to be increasing.
Jack is correct - the angle theta can be measured either CW or CCW, and measured from any line in the xy-plane. That is, there is no normal way to define the angle.