| Problem statement Solution video |
DISCUSSION THREAD
![]()
You can ask questions or answer questions of others here. You can learn from either.
DISCUSSION
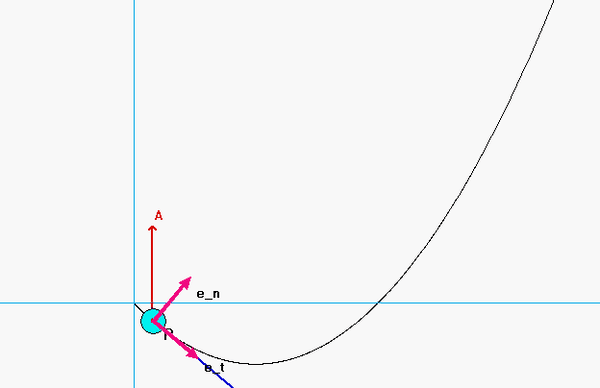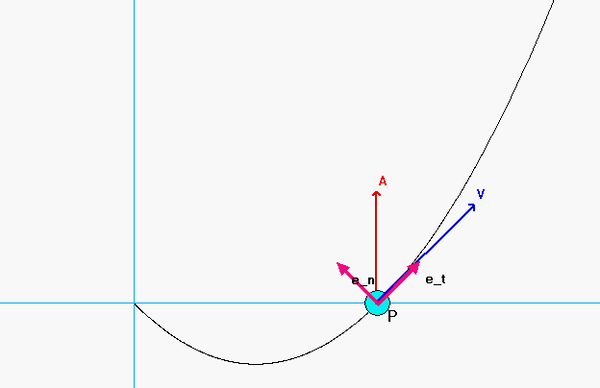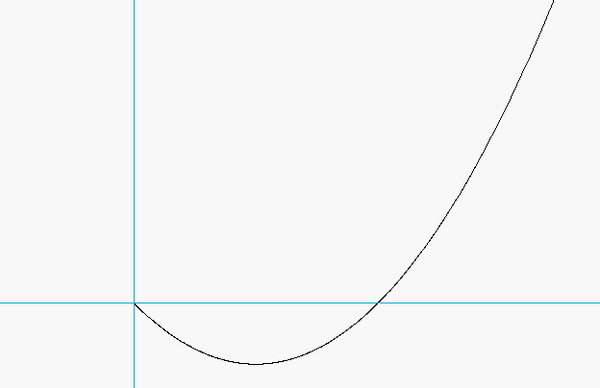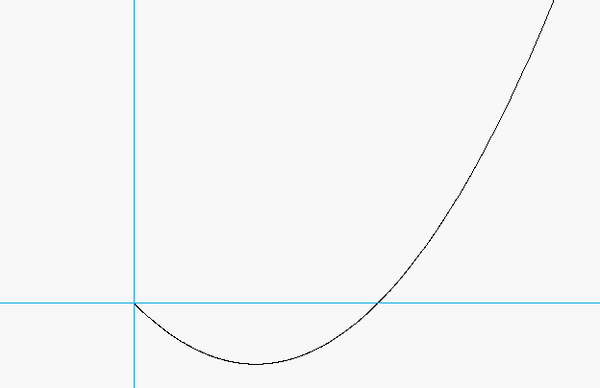
Shown in the animation below is the path taken by Particle P.
- As expected the unit vectors et and en are tangent and normal to the path of P, repectively.
- Also seen there is that the velocity vector is always aligned with the tangent unit vector, et, since v = v et.
- The acceleration vector, in general, has both tangential and normal components of acceleration. The normal component always points in the same direction as the unit normal vector, en. The acceleration vector either points "forward" of the motion (for which the rate of change of speed is positive; i.e., increasing is speed), or points "backward" of the motion (for which the rate of change of speed is negative; i.e., slowing down).
HINTS
Recall that since you do not know the y-component of motion of P explicitly in terms of time, you will need to use the chain rule to find dy/dt.
It is most convenient to determine the rate of change of speed through the vector projection of the acceleration vector, a, onto the unit tangent vector, et. How do you find the tangent unit vector? Simply divide the velocity vector by its magnitude! et = v/v .
Once you know the rate of change of speed, you can find the radius of curvature ρ through the magnitude of the acceleration.
In lecture we used et to solve for rate of change of speed. Can't you also find it by doing (a*v)/|v| with the i and j components or does this not always work?
The two processes are the same thing in disguise because êt = v/|v|
so a*êt = (a*v)/|v|
See hint for a more in-depth explanation: "It is most convenient to determine the rate of change of speed through the vector projection of the acceleration vector, a, onto the unit tangent vector, et. How do you find the tangent unit vector? Simply divide the velocity vector by its magnitude! et = v/v"
Does this problem want us to use cartesian for part b, then move to path coordinates, or is it just strictly one method of solving?
Hi Jack!
To solve this problem I used the cartesian coordinates to solve for velocity and acceleration (part b) and changed to path description for solving for the rate of change of speed (part d).
As Ella mentioned, you will solve in cartesian for part b, but when solving for the rate of change in part d, you will have to change to path coordinates.
When I solved this question, I started by getting all my values with the Cartesian definition. For part B, I projected the cartesian acceleration onto et to finish solving from there.
Yes, that's what I thought was easiest to do.
Hello, I have a question about units. When I solve mine out, i get the final answer in acceleration to be ft^2/s^2. Ive checked my process and I am not sure where I went wrong. A similar problem is in HW 1.B but instead they provide a 1/m factor which gets rid of the extra m allowing for the units to be correct. I was wondering if that was the issue with this problem too.
I am having the same issue. Were you able to figure out what we are missing?
If you look at the equation for the path provided, you can see that (in order to have the right hand side of the equation to be consistently in units of ft):
* The factor of (1/2) has associated with it units of(1/ft).
* The factor of 10 has no units associated with it.
Is this problem y(x) = (x^2)/(2-10x) or y(x) = (x^2/2) -10x?
y(x) = (x^2/2) -10x is the correct one
(x^2/2)-10x
The last hint mentioned finding the radius of curvature. While I was working the problem through, I didn't see a place where finding that value would be necessary. Did I miss something or was that step not needed for this problem?
I assume the hints might have been recycled from a homework where the radius of curvature was included. Since there is nothing on the pdf with the problem, I would assume that we don't need to solve for it.
when adding the acceleration and velocity to the sketch, are we supposed to choose an arbitrary point on the path and show the vectors for that point?
Hi Grace!
The problem specifies that x = 10ft. That's where I drew my particle.
For this problem, are we putting our answers for velocity, acceleration for part b, and rate of change of speed for part c in terms of x, or should our final answer include plugging in x = 10 and the other given values?
I put my final answer after plugging in x=10. I don't think it should be left in variables.
Since the problem specifies x = 10 ft, I plugged in the x-value for all my final answers.
How do we know that the rate of change of speed equals the dot product between acceleration and et? I'm a little confused on where that equation comes from.
The path description for acceleration is given by:
a =(v_dot)e_t + (v^2/rho)e_n
From this, you can see that v_dot is the "projection" of a onto the unit vector e_t:
v_dot = a • e_t
If you do not see that, then just do the dot product.
This is discussed in Section 1.C of the lecture book, and was discussed in lecture.