Chapter 1 Homework

Homework H1.J - Sp 25

16 Comments
Problem statement
Solution videohttps://youtu.be/gVa5DhEtPW4

DISCUSSION THREAD

Ask or answer questions here. You can learn from either.

DISCUSSION and HINTS
Since the cable does not stretch (R_dot = R_ddot = 0), an observer on aircraft A will see a circular path for B, although the true path of B is more complicated than that. Since θ_dot = constant, then θ_ddot = 0.

It is recommended that you write down the relative motion kinematics equations relating the motions of A and B:

vB = vA + vB/A
aB = aA + aB/A

and use a set of polar coordinates to describe vB/A and aB/A:

vB/A = R_dot*eR + R*theta_dot*eθ = R*theta_dot*eθ
aB/A = (R_ddot - R*theta_dot^2)*eR + (R*theta_ddot +2*R_dot*theta_dot)*eθ = - R*theta_dot^2*eR

16 thoughts on “Homework H1.J - Sp 25”

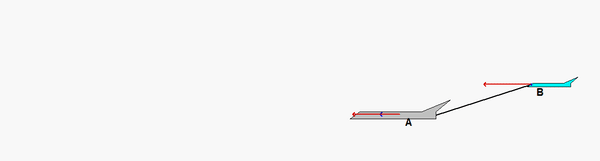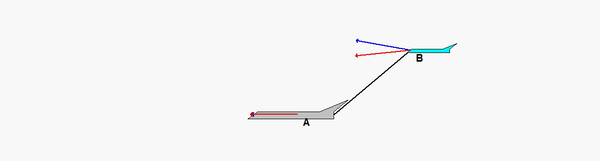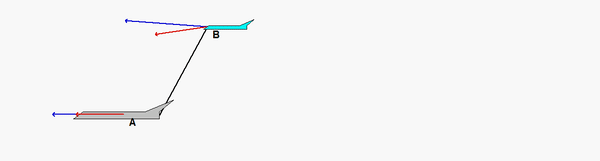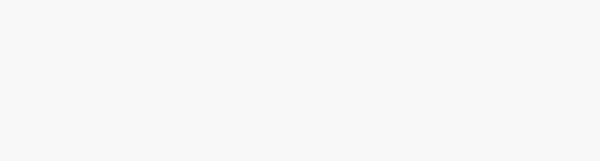
  1. It seems to me that the answer to this problem should be in cartesian coordinates. Is that correct? It does not seem that the problem statement explicitly states

    1. I'm thinking that the answer is going to be in polar coordinates. This thought comes from the fact that we are given a theta dot, a component of velocity and acceleration in polar coordinates

      1. Nevermind, I missed that the x and y axes are drawn. With that information, I agree with you that the answer would be in cartesian

    2. I would agree with your judgment, the way I did it was I converted my e_theta and e_r to cartesian and after I completed the subtraction of the vectors

    3. The answer should be in cartesian coordinates, however your Vb vector will be in polar coordinates because of Vb = R_dot*e_r + R*Theta_dot*e_theta. The idea is then to convert those polar coordinates into cartesian coordinates so that you can use the Vb/a = Vb - Va formula (and in part b using the Ab/a = Ab = Aa)

      1. The way you put this really makes sense to me now, and this is probably a silly question, but how do we find R dot in the equation for polar coordinates of Vb? I know we are given the value of R, but how do you find R dot? Is it not zero?

        1. Since R is a constant (you can assume the cable is inextensible and treat it as a rigid body) R_dot will be zero. It's also stated in the hints when defining v_B/A. v_B/A = R_dot*eR + R*theta_dot*eθ => R*theta_dot*eθ

      2. While I agree with your strategy of converting to either cartesian or polar to add or subtract the relative motions. I am unsure about your statement that aB/A is = to Ab and Aa; Was this a typo? The angle theta is not constant meaning that theta dot is non zero. This leads there to be a relative acceleration between A and B. The equation for aB/A is (aB/A = aB - aA).

    4. for this problem, you must first define local coordinates relative to point B from the perspective of point A. In this case, you should use polar coordinates because B is moving in a circular path around A.
      But then you must convert to global coordinates to find the actual velocity and acceleration of B. This means that you have to convert to cartesian coordinates for your final answer.

  2. Should we convert theta to radians or is degrees alright? I see the theta dot is in radians per second which made me question the units of theta.

    1. I think that when working with theta dot, the unit in rads does not affect the value, but when you are working with the theta value of 30 degrees, you should leave that in degrees instead of radians.

  3. When solving this problem, should we convert from cartesian to polar to get the velocity or acceleration vector and then put it back into cartesian coordinates for the final answer?

    1. Having your final answer in terms of either Cartesian or polar coordinates is fine. Cartesian might make more sense.

    2. It would be easiest to convert the polar coordinate equation of Vb/a into cartesian. This would make your final answer in cartesian coordinates.

    3. The way I did it was I converted from polar to cartesian since it was easier to visualize but if you set up your conversion how they taught us with the table, then you have flexibility on choosing either of the coordinates

    1. The r vector would go from the tail of the plane to point b and the theta vector would be 90 degrees counterclockwise

    2. The r vector would go from the tail of the plane to point b and the theta vector would be 90 degrees counterclockwise

    3. The r vector would go from the tail of the plane to point b, and the theta vector would be 90 degrees counterclockwise from that

      1

Comments are closed.