| Problem statement Solution video |
DISCUSSION THREAD
Ask and answer questions here. Think about helping out someone who has a question. You will learn as you help with a well thought-out answer.
DISCUSSION and HINTS
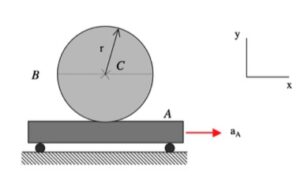
Block A moves to the right with a speed of vA, with this speed changing at a rate of aA. The disk rolls without slipping on the block in such a way that C has a known speed of vC, with this speed changing at a rate of aC.
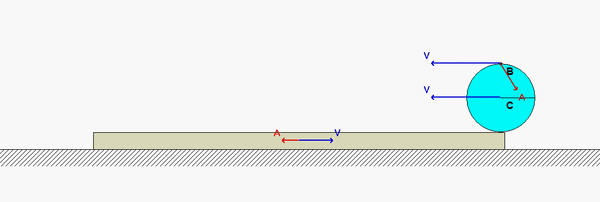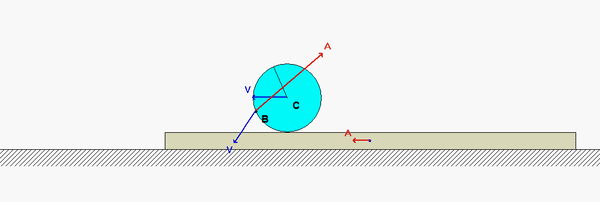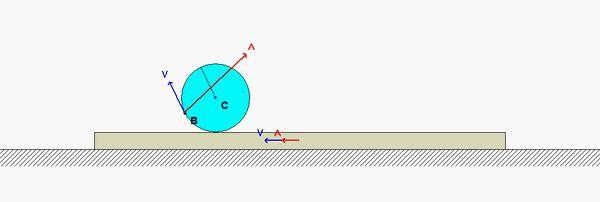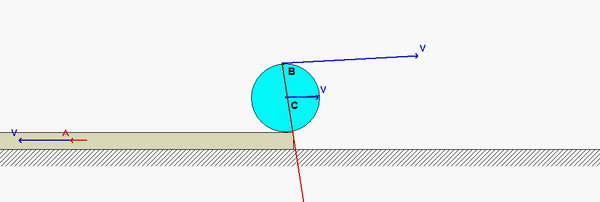
It is recommended that for this problem, you use the following rigid body kinematics equations relating the motion of the center of the disk C and the point on the disk that is in contact with block A (let's call that point E):
vC = vE + ω x rC/E
aC = aE + α x rC/E - ω2rC/E
What do we know about the motion of point E? Point E has the same x-component of velocity and acceleration as does block A. The y-component of velocity of E is zero, but the y-component of acceleration of E is NOT zero. (Do you know why?)
Does point E in the hints refer to the point that is always in contact with block A (so a moving point respective to the disk) or is it equivalent to point B, so just a static point on the rim of the disk?
The point E mentioned here is on the disk. Due to non-slip, E and A have the same horizontal components of velocity and have the same horizontal components of acceleration. The vertical components of acceleration of E and A are NOT the same.
Thank you for the response! So, would this mean that point E and point B are equivalent?
Yes and no. Both B and E are on the outer surface of the disk.
However, for the instant of interest, E is at the contact of the disk with the cart, whereas B is located directly to the left of point C.
Where is point B? Is it to be taken as the leftmost side of the wheel?
I think point B is located on the circumference of the circle on the left side of the wheel so the distance between the center and the point B is r or the radius of the circle.
At any point on the circle the distance between the center and a point on the circumference is r by definition of radius. It just means that there is a 90 degree angle between point B and E
Yes, 90 degrees.
Is point E the same as A' , similar to the notation we used in the examples in class?
Does it matter which point (like C, or E once we find the y component) we use to solve for the velocity and acceleration at B? Will it give the same answer, since they are both known points on the surface?
I had the same question, but I got the same answer after solving it both ways. I hope this helps.
I know that aE has a vertical component aEy, but does aC also have a vertical component aCy?
No. C moves on a straight path in x-direction. Referring back to the PATH description, this means that the acceleration of C cannot have a component perpendicular to the path; i.e., a_Cy = 0.
No, aC does not have a vertical component (aCy) in this case, as the question specifies that aC = (aC)i.
I was wondering if alpha is always -a/r even if the ground is moving or only in some cases?
The equation that you quote above is rarely true for the general problem of rigid body kinematics. You should always start out with the general equation and work from there.
how do we find the angular velocity for this?
To find the angular velocity, we can use the relationship between the velocity of point A' (the point on the disk that touches block A) and the velocity of point C. We want to determine the unknown angular velocity by considering two points for which we already know their velocities. By applying the equation vA' = vC + ω x rA'/C, we can plug in the velocities of points A' and C, allowing us to solve for the angular velocity of the disk.
Should our answer be in terms of vector or magnitude?
Note that velocity and acceleration are vectors. Please report your answers as vectors.
Is velocity at E the opposite direction of the velocity at A?
No. It is in the SAME direction.
Do we need to find the y-component of acceleration for point E? It mentions it in the problem, but we should be able to just isolate the x component in the acceleration equation, right?
Funnily enough, after I posted my question, reading your question gave me the answer to my question. Yes, just using the x-component of a_e will give you the result you need for alpha. Hope this helps.
I get that the problem states that the acceleration of c is in the positive x direction at the given instant, but with the equation for relative motion a_c = a_e + alpha x r_c/e - w^2(r_c/e), wouldn't the w^2(r_c/e) term be in the j direction since r_c/e is +rj_hat? This would imply that there is a j-component for acceleration for c, which I know is wrong. Can someone help me figure out where my logic has gone astray?
I forgot that a_e has a j-component of acceleration and should exactly equal to the w^2(r_c/e) term in the equation so that a_c has a 0-acceleration component in the j direction.
Choosing point E to be at the bottom of the wheel and in contact with the surface, v_e = v_a, and v_e goes in the +i direction. How is it that the velocity at the center of the wheel, v_c, also goes in the +i direction, shouldn't v_c and v_e act in opposite directions?
This is a problem on kinematics. We do not know what external forces that act, and we do not know the mass distributions. All of these factors go into determining the directions of motion and the speeds. We will cover this in Chapter 4. For now, we use the directions of motion that are provided.