| Problem statement Solution video |
DISCUSSION THREAD
Ask your questions here. And, consider answering questions of your colleagues here. Either way, you can learn.
DISCUSSION and HINTS
In this problem, end A of the bar is constrained to move along a straight horizontal path with a constant speed of vA, whereas end B is constrained to move along a straight, angled path. As you can see in the animation below of the motion of the bar, the speed of B is NOT a constant (the acceleration of B is non-zero, and is, in fact, increasing as B moves along its path).
In your solution, it is recommended that you use the rigid body kinematics equations relating the motion of ends A and B:
vB = vA + ω x rB/A
aB = aA + α x rB/A – ω2rB/A
For these equations, you know: i) the magnitude and direction for the velocity of A; ii) that the acceleration of A is zero (constant speed along a straight path); and, iii) the direction for the velocity and acceleration of B. These two vector equations produce four scalar equations that can be solved for four scalar unknowns: vB, aB, ω and α.
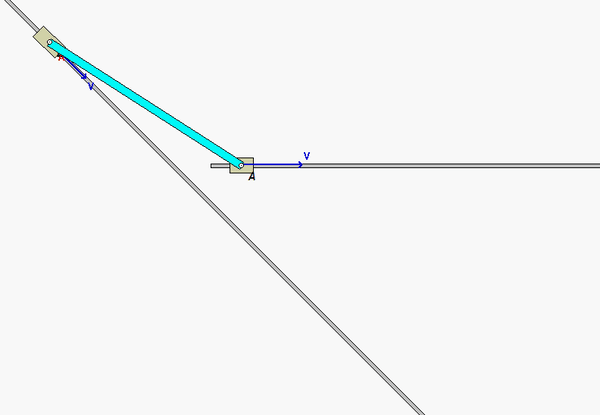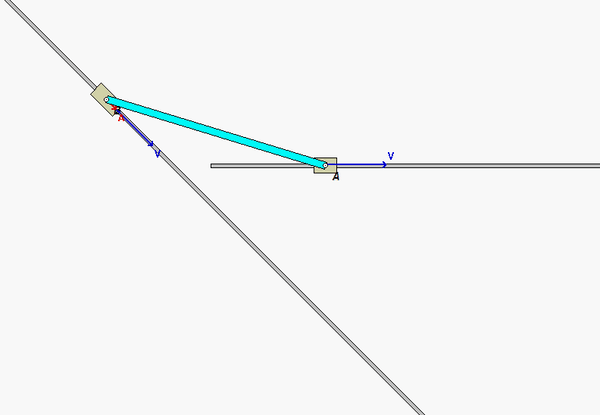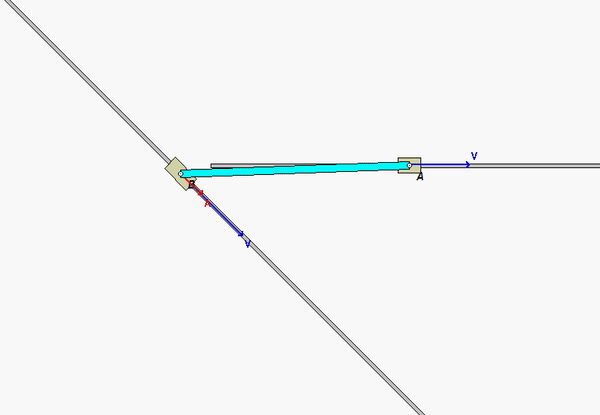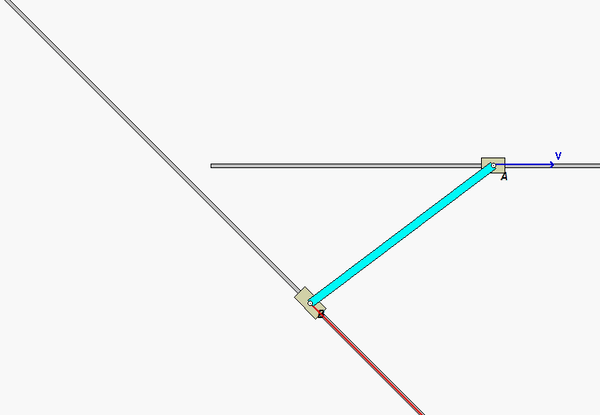
How does phi affect the problem?
I’m pretty sure that since B is on an angled plane rather than vertical (like in the lecture book) we have to accommodate for the slant. So when you’re solving for velocity and acceleration you’ll have components for both i and j rather than just j.
The acceleration for A would just be zero since Va is a constant right?
Yes that’s correct
Because of constant speed AND a straight path.
The angular velocity, ω, is an unknown. Usually it is equal to theta_dot k. With this problem including two angles, does this change ω? Same question for finding α.
omega is the angular velocity of the bar. There is only one omega for the bar.
I got two equations for velocity and acceleration each. There were two unknowns for velocity equation which were omega and vb. For acceleration, angular accerlation and ab were the unknowns.