Chapter 2 Homework

Homework H2.E - Sp 25

16 Comments
Problem statement
Solution video

DISCUSSION THREAD

Ask and answer questions here. Give your colleagues some help with thoughtful responses. You can learn for that experience.

DISCUSSION

As you watch the animation below, you see that C moves back and forth along a straight path. In general, C has a non-constant speed; therefore, with the path of C being straight, its acceleration is always directed along the path of C. Point B, on the other hand, moves along a circular arc path with a non-constant speed. Owing to the curvature of the path of B, the general acceleration of B is directed neither purely tangent nor purely normal to the path of B. Using our earlier understanding of the path description of motion, the normal component of acceleration of B is due to the centripetal term of vB2/r. Note in the animation that for positions of B for which vB = 0, the acceleration of B is tangent to the path.

 

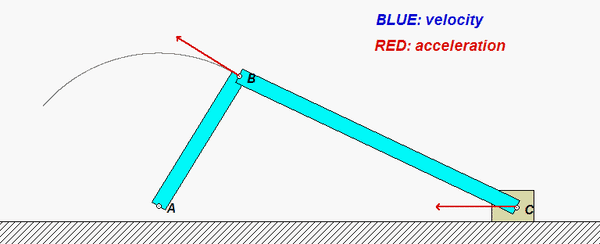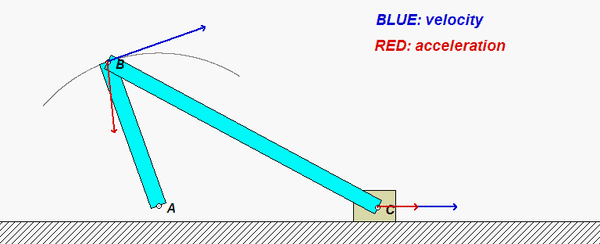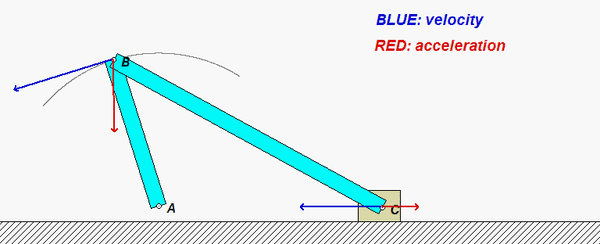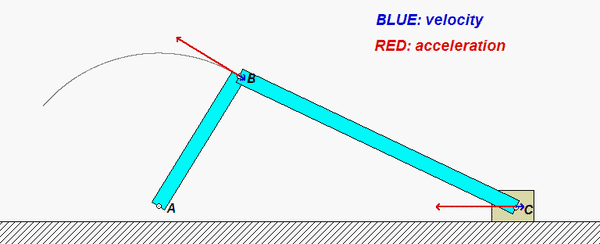
HINTS
Velocity analysis
As recommended in lecture, we should write down a rigid body velocity equation for each rotating link in the mechanism. For this problem, we should use:

vB = vA + ωAB x rB/A
vB = vC + ωBC x rB/C

For these two equations, we know both vA(= 0) and vC . Equating these two equations gives two scalar equations in terms of ωAB and ωBC .

Acceleration analysis
Similarly for acceleration, we should use:

aB = aA + αAB x rB/A - ωAB2rB/A
aB = aC + αBC x rB/C - ωBC2rB/C

For these two equations, we know both aA(= 0) and aC . Equating these two equations gives two scalar equations in terms of αAB and αBC .

16 thoughts on “Homework H2.E - Sp 25”

    1. I got a link BC angular velocity of zero using directional dot products. Based on the movement in the model, I think the velocity of BC is entirely due to the rotation of link AB so the link
      BC is just translating without rotation at the given moment.

      1. Thank you! I also ended up getting that wBC was 0 but I wasn't sure if it actually made sense for the problem.

    1. No, I do not think we can assume the angular acceleration of link AB to be zero. Since AB is pinned at A, it undergoes pure rotational motion. The velocity of B is influenced by the motion of C, which moves horizontally with a given velocity and acceleration. Using velocity and acceleration relations, we see that point B has an acceleration component due to point C’s motion. Hope this helps!

      2

    2. Assuming zero angular acceleration would not be a wise choice. If it is zero, your math will tell you that. There are few assumptions that you need to make in solving homeworks in this class, outside of what are given to you in the problem statements.

    3. We cannot assume the angular acceleration of AB to be zero because the equations used for calculations are only for this specific instant where AB is vertical and C is moving to the right. However, for point C to start moving in the opposite direction there has to be translational deceleration, due to which angular acceleration cannot be assumed to be zero. There is also no evidence to suggest that the angular acceleration will be zero. We can only assume that angular acceleration is in the k direction because we are dealing with a 2D system.

  3. Do we report the final answer for angular in the k vector, or is it the i or j vector that we got the answer from

    1. Since all of the translation for the rigid bodies in this mechanism is completely in the xy-plane, the rotation of each link is about the k-axis (perpendicular to the xy-plane).

  4. I am a bit confused what to do next, I have gotten two equations for VB, one in terms of wAB, and wBC, if I set these equal to eachother I'm just confused in how to solve for each angular velocity because it seems like I have too many unknowns, is there a step I'm missing?

    1. No, you are not missing a step. You should be able to set them equal to each other and then create two equations an i, and j equation. You will then have two equations for two unknown variables.

      1

    2. You should get 1 equation for Vb, and one equation for Vc(which include the Vb component). So its technically a sort of a system of equations which you then solve by seperating the i and j components like we did in the previous homework.

    3. I think from here what you need to do is separate the equations into their i and j components and solve from there.

  5. You do not need to make a new system of reference because the original vc is just in the i direction

  6. Would it make sense for the angular velocity of AB to be negative? Any recommendations on how to intuitively know which direction it should be going?

    1. As C moves to the right, so does point B. If B moves to the right, then AB is rotating in the CW direction about point A. If you initially wrote the angular velocity of AB in the following form, omega_AB = omega_AB*k_hat, then CW is in the negative direction by the right hand rule.

      Make sense?

Comments are closed.