| Problem statement Solution video |
DISCUSSION THREAD

Ask and answer questions here. Helping a colleague with their questions is often as educational as is asking questions yourself.
DISCUSSION and HINTS
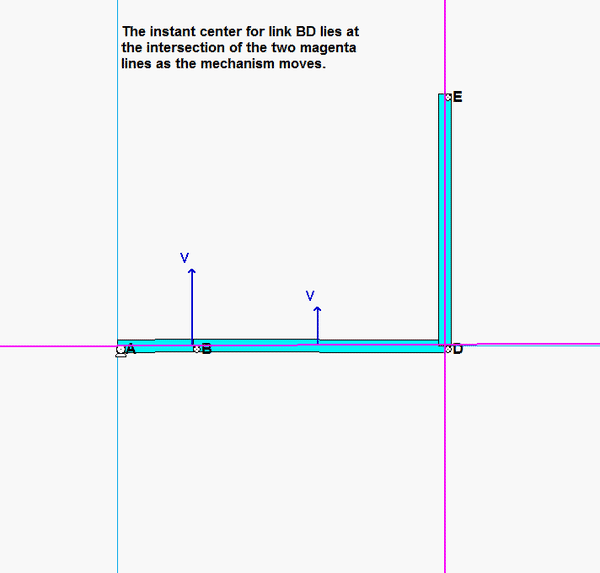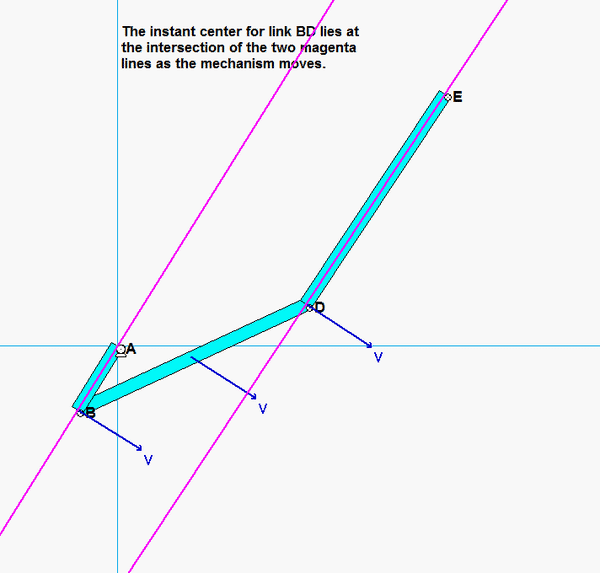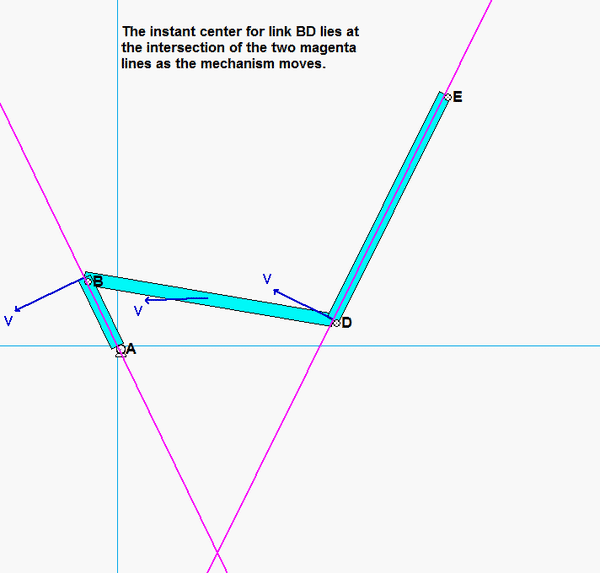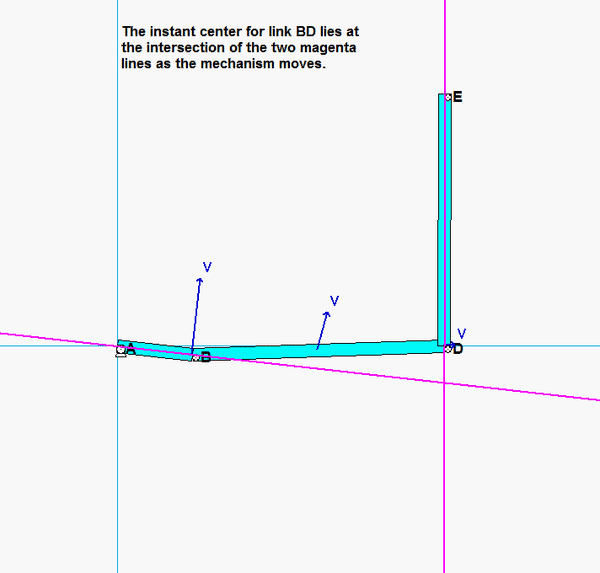
As discussed in lecture, we can locate the instant center (IC) for a rigid body through knowledge of the direction of motion for two points on that body. Here, we want to know the location of the IC for link BD. To this end:
- The path of B is circular with its center at A. Therefore, the velocity of B vB is vertical.
- The path of D is circular with its center at E. Therefore, the velocity of D vD is horizontal.
- Draw a line that is perpendicular to vB , and draw a line that is perpendicular to vD. The intersection of these two perpendiculars is the IC for link BD. See the animation below that shows how the location of the IC for for BD moves as the mechanism moves. It is called the "instant" center because its location changes from instant to instant.
Recall, also, that the speed of any point on a rigid body is equal to the angular speed of the body times the distance from that point to the IC for that body. This provides you with the equations needed to find the angular velocities of links BD and DE.
Why is the angular velocity of AB = -4 rad/s if it appears to be rotating counter-clockwise as depicted by the video and the arrow. Isn't CCW (+) by the right hand rule.
The animations have been created for a generic set of parameters such as rotation rates and directions. We change the magnitudes and directions of the rotation rates from time to time in the homework assignment itself.
The actual location of the IC for link BD is independent of the actual direction of motion, be it CW or CCW.
As you observe here, it appears that this animation was created using omega_AB = +4 rad/s (CCW).
Thank you,
So for the problem givens, a (-) angular velocity of BD fits mathematically.
Is it true that the instant center will have velocity = 0 at the given time?
By my understanding, yeah the instant center should have zero velocity at that point in time. If you think about this mathematically, the velocity from a points instant center is the distance of that point from the instant center times the angular velocity of the object. In this case if we consider the instant center to be the point, then it has zero distance from itself meaning that its velocity is zero times the angular velocity.
Do we need to know the direction (sign) of v_b at any point in this problem? I found that I got my answers without that but I am not sure if that is right.
I also didn't need the sign of V_b.
Since the the angular velocity of AB is in the counter clockwise direction, the direction of vb would be upwards being influenced by that angular velocity, but it is not really needed in this problem, just knowing that it goes up or down makes you able to draw construction lines and obtain the location of the instant center.
You can use the magnitude of Vb initially for your equations to find other unknowns and then the sign will come from how it should be drawn in the picture. But since the diagram starts with the angular velocity of AB being counter clockwise the Velocity of B will point upward to match this
I'm still confused about the correct orientation for omega_BD. omega_AB was shown to rotate in the CCW orientation yet the value was -4 rad/s. Based of my IC_BD at this state and V_B, I believe that omega_BD should rotate in a CW orientation, yet by the math I also get a negative rad/s value. Is this fine that omega_AB and omega_BD both have the same sign, yet the appear to rotate in opposite directions?
If you assigned BD a CW orientation while AB has a CCW orientation in the diagram then, assuming you kept those orientations in your calculations, both omega values being negative would indicate they still both move in opposite rotations with BD being CCW and AB being CW.
Would drawing the Instantaneous Center on the model be enough for part a?
Yes. That is all that is asked for Part a).
If Wab is negative why does it rotate CCW in the animation?
I believe Prof. Krousgrill answered this earlier, but it is because the animations are of general application to the problem. Values, signs, or directions are often changed on homework problems.