| Problem statement Solution video |
DISCUSSION THREAD

Ask and answer questions here through Comments. You can help others with thoughtful responses to their questions. And, you can learn from the process of doing so.
DISCUSSION and HINTS
This mechanism is made up of three links: AB, BC and the wheel. You are given the constant rotation rate of link AB, and are asked to find the angular velocities and angular accelerations of link BC and of the wheel.
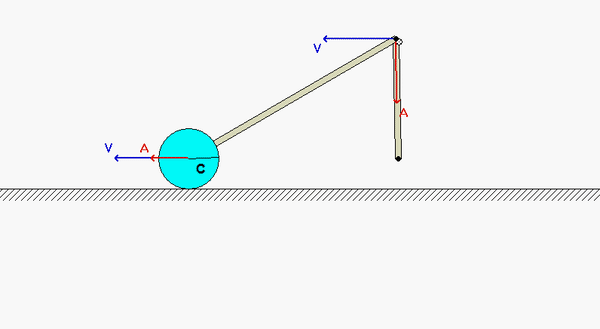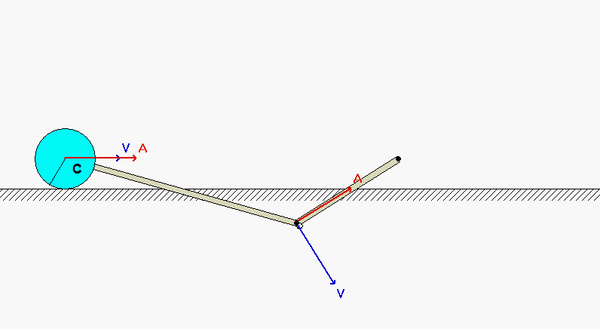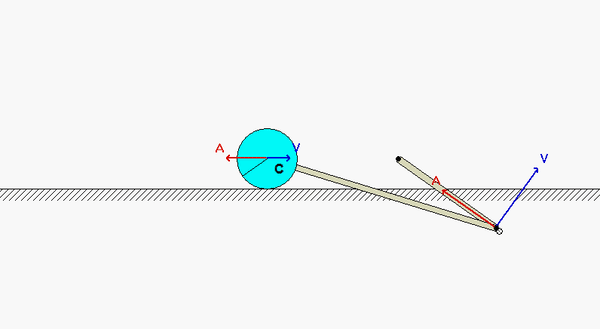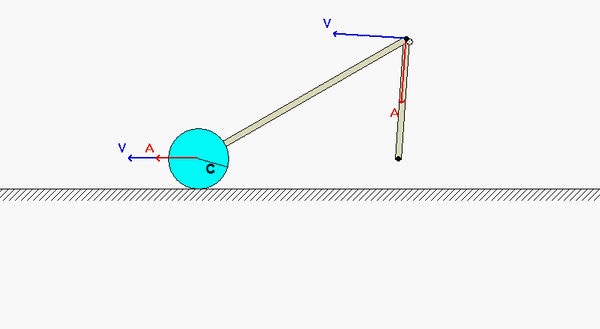
Velocity analysis
Where is the instant center of link BC? What does this location say about the angular velocity of BC?

Acceleration analysis
Write a rigid body acceleration equation for each of the three links in the mechanism:
aB = aA + αAB x rB/A - ωAB2rB/A
aC = aD + αwheel x rC/D - ωwheel2rC/D
aB = aC + αBC x rB/C - ωBC2rB/C
where D is the point on the wheel in contact with the ground. Note that the horizontal component of aD is zero, whereas the vertical component of aD is not zero. Combining together these three vector equations in a single vector equation will produce two scalar equations in terms of αwheel and αBC .
Is the point D discussed in the notes supposed to be point E on the wheel?
No, D is the point on the wheel in contact with the ground.
No, D is the point at which the wheel is in contact with the ground.
How do you find the vertical acceleration at point D? I have two scalar equations in terms of the acceleration at D and the two angular accelerations, but I can't figure out how to get rid of the acceleration at D.
I also need help with that, same as you I found the two equations in the I and j directions in terms of the angular accelerations of the wheel and BC but do not know how to find vertical value of aD.
When you write down the acceleration equation relating points C and D, you will have one unknown for the acceleration of D (since for no-slipping, the horizontal component of acceleration of D is zero). You should have enough equations to solve for your unknowns.
For my equation relating C and D, I get an equation for a_c in terms of a_d and α_wheel, and then two equations for a_b, one in terms of a_c and α_bc, and the other just as a number value. I substituted in that a_c equation into the first a_b equation and then set the two a_b's equal, but then in both directions I get two unknowns, one with both angular accelerations, and then one with a_d and α_bc. I can't figure out what I'm missing?
Y'all don't need to solve for the vertical value of aD. With the final equation of ac, you can separate the components into i and j. Then you only need the i components to find the angular acceleration of the wheel.
Is this because ac has no j component so when we make the ac relative to ad equation we can just look at i component?
Would it be true that at the given instant, the velocity at point D would be 0?
Since this is a no-slip situation, point D will have the same velocity as the ground it is touching, so yes.
Yes, the contact point D will have zero velocity.
Yes, with no slip the instantaneous velocity of the point on the wheel that is touching the ground is 0 - obviously assuming the ground is not moving. In some of the other examples where the ground is moving relative to the wheel the point on the wheel touching the ground has whatever velocity that the ground does.
Is the angular velocity of the wheel found through the formula omega_wheel = v_c/r(c/d)?
Yes, you could also just use Vb as it has the same velocity as the center of the wheel (in the x direction at least).
I have an answer for Vb that only has an i quantity. However, when examing how the system would move, I would expect it to also have a j component. Is it correct to assume Vb should also have a j component?
Keep in mind that point B has a circular path, with the center of circle at A. When AB is vertical, then the tangent to this path is horizontal. Because of this, the velocity of B should have only an i-component.
Make sense?
When finding WBC, I already found VB using WAB (which is known), so know i'm guessing I use the known VB = unknown WBC * some length to find WBC, but im not sure what that length would be? Would it be L?
Just use the standard rigid body velocity equation relating the motion of B and C:
vC = vB + omega_BC x r_C/B
Following up on a question posed in the above discussion: Where is the IC for link BC? That will tell you what the angular velocity of BC is.
Why do we use Ab=Ac+alphaBC x r_b/c - w_bc^2 * r_b/c instead of Ac=Ab+alphaBC x r_b/c - w_bc^2 * r_b/c?
I keep getting a negative value for alpha_cd, but the gif shows the motion of the wheel is ccw rotation. After solving for my i components and j components, I'm left with alpha_cd = (-alpha_bc * d)/r. Any ideas as to where I could've gone wrong?
Yes, the animation shows a CCW angular VELOCITY; however, if you study this motion carefully, you will see that the angular velocity is decreasing. This implies that the angular acceleration is CW.