Chapter 2 Homework

Homework H2.J - Sp 25

9 Comments
Problem statement
Solution video

DISCUSSION THREAD

Ask and answer questions here. Help others with thoughtful responses to their questions. You will learn from the experience.

DISCUSSION and HINTS
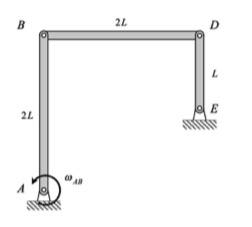
This mechanism is made up of three links: AB, BD and DE. You are given the rotation rate of link AB, and are asked to find the angular velocities and angular accelerations of links BD and DE. At the position shown, it is known that ωAB = constant.

From the animation below, we are reminded that B and D move on circular arc paths with centers at A and E, respectively. The velocities of B and D are always perpendicular to the lines connecting the points back to the centers of the paths. Can you visualize the location of the instant center (IC) of link BD as you watch this animation? For the position of interest in this problem, you see in the animation that the velocities for all points on BD are the same - is this consistent with the location of the IC for BD at that position?

Velocity analysis
Where is the instant center of link BD? What does this location say about the angular velocity of BD?

Acceleration analysis
Write a rigid body acceleration equation for each of the three links in the mechanism:

aB = aA + αAB x rB/A - ωAB2rB/A
aD = aE + αDE x rD/E - ωDE2rD/E
aB = aD + αBD x rB/D - ωBD2rB/D

Combining together these three vector equations in a single vector equation will produce two scalar equations in terms of αBD and αDE.

9 thoughts on “Homework H2.J - Sp 25”

  1. Since the velocity of B and D move in the same direction, doesn't that mean there is no instant center for BD?

    1. To be more precise, the perpendiculars for the velocities of B and D intersect only at infinity. So there is an IC for BD. This then says that omega_BD = 0.

  2. Because there are no numerical values given for angular velocity of AB, can we just leave our answers including Wab in vector form?

  3. Can we assume that a_D is purely in the j direction? If so, why can we assume this? How do we know that there is no horizontal acceleration?

    1. I would recommend against such an assumption. If the acceleration of D is only in the j-direction, then your math will tell you that. No need to assume.

      Have faith in your math. 🙂

  4. I know that the angular accel of AB = 0 because angular vel. of AB = const. which was given in the problem statement. Is this fair to assume for angular accel of BD because angular vel. of BD turned out to = 0? Just wondering if a 0 velocity equates to 0 accel even though this is just the velocity at this instant, and it could still be changing.

    1. I don't believe that we can assume this. It would seem that at another moment in time, BD would have a nonzero angular velocity indicating angular acceleration.

    2. Do not assume that the angular acceleration of BD is zero just because the angular velocity is zero. like a wheel that is not slipping, at one instant, the velocity will be zero however there must still be an acceleration to change the velocity to nonzero. If the velocity and acceleration is zero, then the object is not moving at all.

Comments are closed.