| Problem statement Solution video |
DISCUSSION THREAD

Ask and answer questions here. Either way, you will learn.
DISCUSSION and HINTS
In this problem, we desire to relate the rotation rates of link OA and the disk.
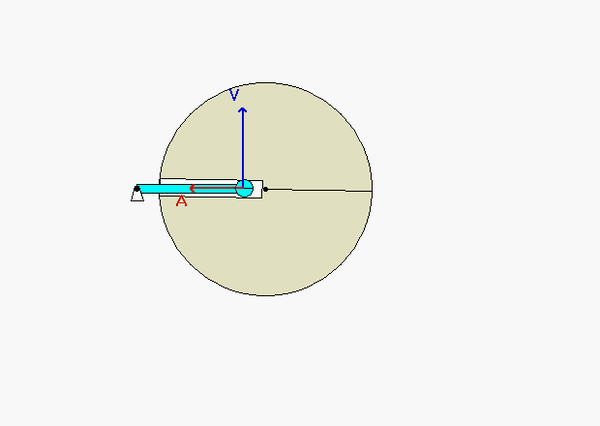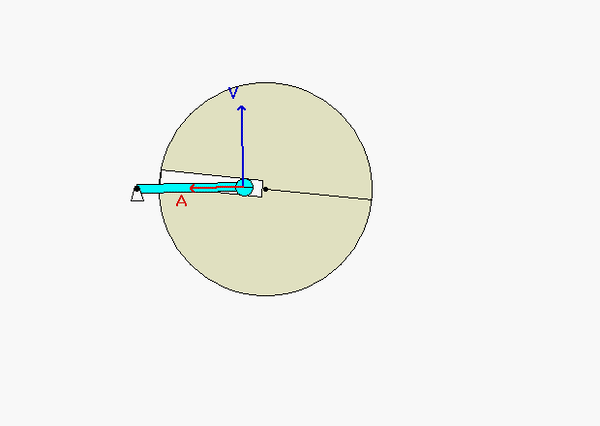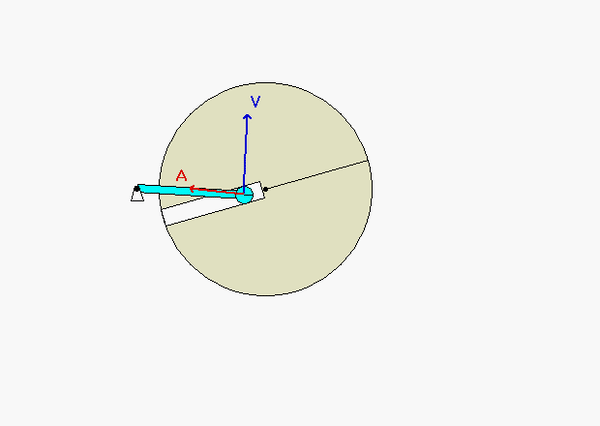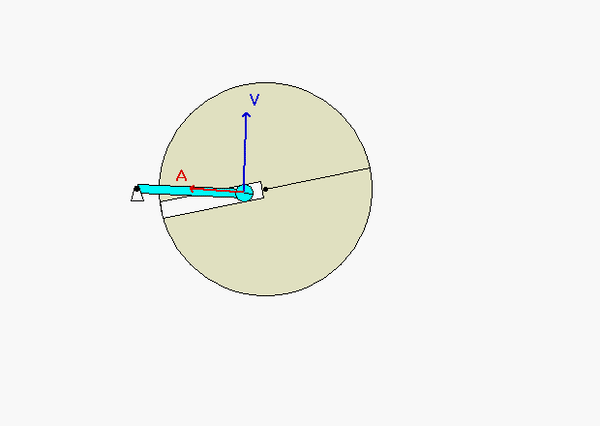
With the two rigid bodies connected by a pin-in-slot joint, we are not able to use the previous rigid body kinematics equations by themselves. Let's discuss that below.
Velocity analysis
Here, we can use the rigid body velocity equation to relate the motions of O and A:
vA = vO + ωOA x rA/O
However, we cannot use a rigid body velocity equation to relate the motion of points A and B (the reason for this is that A and B are not connected by a rigid body). In its place, we can use the moving reference frame velocity equation with an observer attached to the disk:
vA = vB + (vA/B)rel + ω x rA/B
where ω is the angular velocity of the observer, and (vA/B)rel is the velocity of A as seen by our observer on the disk. Note that with the observer being attached to the disk, this observer sees motion of A only along the slot.
Combine these two equations to produce two scalar equations.
Acceleration analysis
We will use the same procedure for acceleration as we did for velocity - use a rigid body equation for OA and a moving reference frame equation relating A and B.
aA = aO + αAOx rA/O + ωAO x (ωAO x rA/O)
aA = aB + (aA/B)rel + α x rA/B + 2ω x (vA/B)rel + ω x (ω x rA/B)
where α is the angular acceleration of the observer, and (aA/B)rel is the acceleration of A as seen by our observer on the disk. Again, note that with the observer being attached to the disk, this observer sees motion of A only along the slot.
Combine these two equations to produce two scalar equations.
How can we find V of A relative to B? I understand it moves along the slot, but I feel like I am missing a value that would allow me to know the magnitude
That is one of the unknowns in the problem.
For velocity:
* Write a rigid body equation for link OA.
* Write a moving reference frame equation relating points A and B.
* Balance the coefficients for the two equations, giving you two equations in terms of two unknowns: omega_disk and (v_A/B)_rel.
Repeat the process for acceleration to give you two equations for the two unknowns: alpha_disk and (a_A/B)_rel.
Is the velocity of B zero?
Yes, B is pinned to ground.
I'm a little confused about how to find the i and j components of the (a_A/B) rel unit vector for the second part.
For part a I used the knowledge that the (V_A/B) rel unit vector would be tangent to its circular path. But when I look at the hints animation the acceleration doesn't seem to follow this same logic.
So I'm ending up with 2 equations and three unknowns. My unknowns being (angular acceleration), ( (a_A/B)rel (i component)), and ( (a_A/B) rel (j component)).
With the observer attached to the disk, the motion of A as seen by this observer will be along the straight, radial slot that is cut into the disk.
* The (v_A/B)_rel is therefore along the slot. Write out this as a vector in terms of a set of xy-axes that you attached to the disk, with an unknown magnitude. Let's call that magnitude v_rel. When you combine this equation with the rigid body equation for OA, you will have two unknowns: omega_disk and v_rel,
* The (a_A/B)_rel is therefore along the slot since the slot is straight. Write out this as a vector in terms of a set of xy-axes that you attached to the disk, with an unknown magnitude. Let's call that magnitude a_rel. When you combine this equation with the rigid body equation for OA, you will have two unknowns: alpha_disk and a_rel,
Could the relative velocity ((v_A/B)_rel) be attained by projected the absolute velocity vector of A onto the straight line between A and B?
No. That would give you the projection of the velocity of A onto the direction of the slot. Not sure what that would represent; however, it would NOT be the velocity of A as seen by the observer on the disk.
It is recommended that you follow the plan suggested above, as that plan will work for you on the problems in Chapter 3.
How am i supposed to find the distance of rA/B would the angle be the same and would i use the 300mm and 200mm to find the rA/b.
I would used trig to find the distance between A and B. At this instant, the distance between A and B is not the same as the distance from O to A if that is what you are asking.
The distance from B to A can be found from the law of cosines using the triangle of OAB.
You can find using trigonometry concept, the x axis of rA/B is going to be 300-200cos(theta) and the y axis of rA/B is going to be the same as the y axis of OA
When solving for the acceleration of A from the observer ((a_A/B) rel), is it okay to leave my answer in magnitude form or does it have to be in vector form?
Since acceleration is a vector, your final answer should be written as a vector.
When doing problems like these, I found that when I use that velocity equation with the relative velocity, I write some vectors in terms of lowercase i and j, and others in terms of the stationary vectors, I and J. And then I convert them all into lowercase or uppercase. Is this way of solving valid and not needlessly inefficient?
Does it matter if you were to write your answer in the relative i and j components vs the fixed i and j components?
Either is fine. Be sure that ALL components are in terms of one set of coordinate axes or the other. If they are mixed, you cannot add them together.
For this problem, should (v_ab)rel be found using intuition and knowing that the vertical component of the v_a can be disregarded with certain reference frames rather than found by plugging into a general equation?
Does it matter which coordinate system, the final answer is in?
Should we convert mm to m when solving for rA/B?
I think the key to solving this problem is setting a variable to represent the distance between A and B and using that to represent the position vector between A and B. Also using that variable we can find the relative speed and relative acceleration of particle A relative to B. Also, the question is asking to find the acceleration of pin A as seen by observer on the desk, so we are eventually finding a_rel instead of just the acceleration of A