| Problem statement Solution video |
DISCUSSION THREAD
Ask and answer questions here. And, learn from both.
DISCUSSION and HINTS
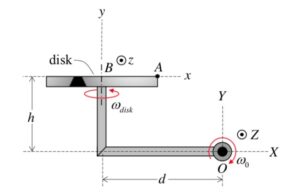
For your work on this problem, it is recommended that you use an observer attached to the disk. The observer/disk has two components of rotation:
- One component of ω0 about the fixed K-axis.
- The second component of ωdisk about the moving j-axis.
Write out the angular velocity vector ω in terms of the two components described above.
Take a time derivative of ω to get the angular acceleration α of the observer/disk. When taking this derivative, you will need to find the time derivative of the unit vector j. How do you do this? Read back over Section 3.2 of the lecture book. There you will see: j_dot = ω x j, where ω is the total angular velocity vector of the disk that you found above.
Acceleration of point A
The motion of A is quite complicated. To better understand the motion of A, consider first the view of point A by our observer who is attached to the disk - what does this observer see in terms of relative velocity and relative acceleration: (vA/B)rel and (aA/B)rel?
With this known relative motion, we can use the moving reference frame acceleration equation:
aA = aB + (aA/B)rel +α x rA/B + 2 ω x (vA/B)rel + ω x (ω x rA/B)
In finding the acceleration of B, aB, note that B moves with a constant speed on a circular path centered on point O. Use the path description to find aB. WARNING: Although B moves with a constant speed, its acceleration is NOT zero.
Is the omega not in the k direction?
omega_0 is in the negative K (upper case) direction; that is, about a fixed axis.
omega_disk is in the positive j (lower case) direction; that is, about a moving axis that is attached to the disk.
w_o will be in the negative K direction and w_d will be in the positive j direction. This is found using the RHR.
Aren't A and B on the same rigid body, so wouldn't the relative acceleration and velocity be disregarded when solving for acceleration at A?
Since the observer is attached to the disk, then all points on the disk are seen by the observer to be stationary. With that, the relative velocity and relative acceleration terms for A are zero.
I'm a little confused and might just need some clarification. When I'm finding the acceleration of B its on a rigid body with O. Can I just use the rigid body kinematic equation to find acceleration of B?
Yeah, you can. And then use that equation to solve for acceleration of A.
When taking the cross products in finding the acceleration of A would you use the angular velocity and acceleration I found in the previous step and cross them with R a/b?
Yes, when finding the cross product you would use the omega and alpha of the disk you found in the previous step.
With the observer attached to the disk, you will have three terms that add together to form the acceleration of A:
* the acceleration of B: a_B
* alpha x r_A/B
* omega x (omega x r_B/A)
where omega and alpha are the angular velocity and angular acceleration, respectively, of the disk (which you found in Part a).
would little i and j still be equal to big I and J even though they don't have the same origin
Yes. Unit vectors represent only directions.
How would you figure out aA/B)rel in this problem?
I believe that (aA/B)rel would just be zero in this problem because A and B are on the same rigid body. I could be wrong though.
I would add to Bella's comment that A is on the same rigid body as the observer.
Using path to find aB, wouldn't the answer be zero?
I am having trouble finding Ab, (Which i'm solving for to plug into Aa), I have tried setting up the path description for Ab, and I know that v dotB will be zero, and I know how to find the radius of curvature, but I am slightly confused on how to find vB?
Instead of using the path description to find A_b you can use the rigid body kinematics equation:
a_B = a_O + alpha x r_B/O - omega^2 * R_B/O
To find r_B/O you would use Pythagorean's Theorem with h and d
Omega is the omega of the arm (omega_0)
Since Point O is fixed, a_O = 0
alpha = 0 since omega_0 is constant
Sorry, you don't even need to use Pythagorean's theorem for r_B/O, you can just leave it split into components h and d
For the path description, you know that the speed of B is the distance between O and B times omega_0.