| Problem statement Solution video |
DISCUSSION THREAD

Ask and answer questions here. You learn both ways.
DISCUSSION and HINTS
Shown below is a simulation of an experiment of dropping a ball onto a fixed surface. Before impact and after impact, energy is conserved. During impact, a large impact force is generated. Although we cannot calculate the details of the force during impact, we can use the impulse/momentum equation to calculate the average force during impact. Note that this experiment differs from your problem in terms of the duration of the impact, with your impact duration being only 20% of the duration shown here.
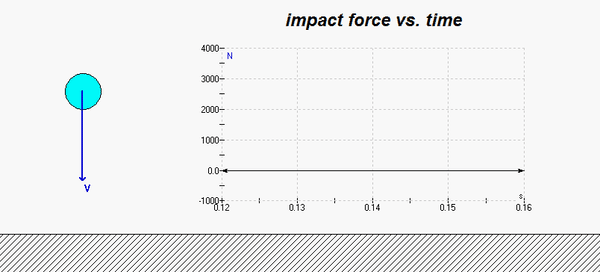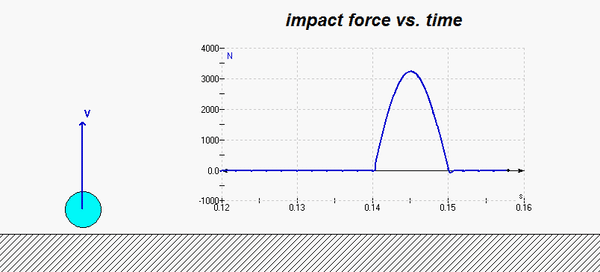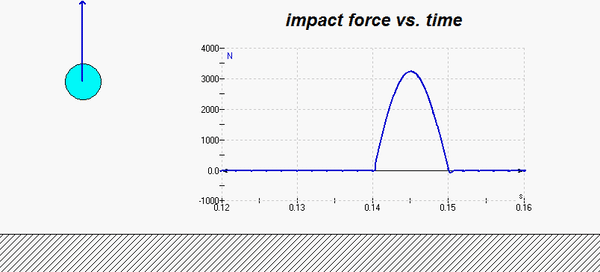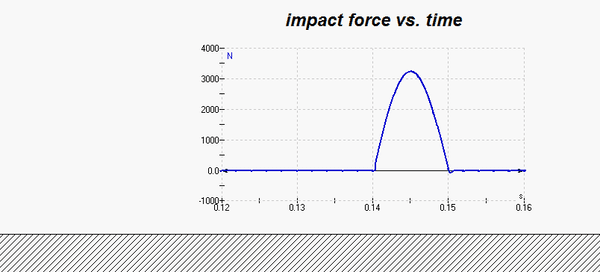
Parts (a)-(c)
Draw two FBDs for the duration of time that includes only the impact: one FBD with weight, and one without weight. Sum forces on the particle in the vertical direction. Use the linear impulse/momentum equation relating the change in linear momentum during the impact to the impulse of the forces acting on the particle during impact. Compare your with and without gravity answers.
Part (d)
Although energy is not conserved during impact, energy is conserved prior to and after impact. Use conservation of energy before and after impact to relate h1 and h2.
Should we ignore air resistance, ie would the only force on the FBD be the force of gravity? In that case, would be no forces on the second FBD since we are ignoring gravity?
Do not include air resistance (no information provided on that here).
What about the normal force? Isn't that the whole thing that part a) is asking about?
During impact, two forces act on the particle:
1)Normal force exerted by the floor, acting upward.
2) Weight () acting downward.
If energy is not conserved during the impact, i.e. some of the mechanical energy was lost due to the impact, how can it be conserved in a time interval which includes the impact (from h1 to h2)?
Energy is conserved only between the initial state and immediately before impact, and between immediately after impact and the maximum rebound height.
Between immediately before and immediately after impact, energy is not conserved.
Outside of the short impact duration, the only force acting on the particle is gravity. Gravity is a conservative force, meaning it does not dissipate energy but simply converts it between kinetic and potential forms. This allows us to apply the principle of conservation of energy separately for the free-fall phase (from height h₁ to the point of impact) and the rebound phase (from the impact to height h₂). The decrease in height (h₂ < h₁) indicates the energy lost during the impact.
Could you also use the kinematics equation vf^2 = v0^2 = 2ay to solve for part d?
Yes, you can use the kinematic equation vf^2 = v0^2 = 2ay to solve for the height ratio. You would apply it separately to the falling and rebounding motion, and derive expressions for the initial and final heights in terms of velocity and acceleration, leading to the same relationship between the two heights.
You probably shouldn't use that equation because they don't want it solved that way.
I would use the W/E equation: T2+V2=T1+V1+U(nc) to relate the kinetic and potential energies because you know some are zero which should setup before and after impact equations to combine for the height ratio.
Not quite sure why you would use this equation. The equation is actually the work energy equation (kinetics, not kinematics) for this simpler problem. If there were more forces acting than gravity, the equation would no longer be valid.
How do I determine if the speed of the particle is 0 at t=0 or halfway through the time interval?
that should not matter. You are initially solving a and b with the linear impulse momentum equation (mv2=mv1+int(sum of forces) wrt time). you solve for f avg with the velocities given to you. they say that those velocities are right before impact. then you can do an energy balance for the rest of the problem.
For part C, do we have to say if the compared force is negligible or not?
4
For part c, when it is asking for us to compare answers, what exactly is it asking? Should we go into detail about the effects of gravity or is a simple comparison enough? I assume we should include some reasoning as to why we can neglect weight, given the large impact force calculated.
The overarching point of the problem is to assess the dynamic effects of the contact point as compared to what you would have for equilibrium. There are a number of points that you might address here.
Is the static contact force significant when compared to the dynamic force?
If the dynamic load is large, what parameter(s) in the problem is (are) responsible?
Based on this one result, do you feel that neglecting weight during impact would make a significant change in the result?
Feel free to discuss in any way that makes sense to you.