| Problem statement Solution video |
DISCUSSION THREAD
Ask and answer questions here. You learn both ways.
DISCUSSION and HINTS
Recall the following four-step plan outline in the lecture book and discussed in lecture:
Step 1: FBDs
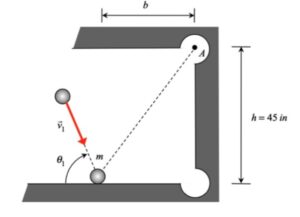
Draw a free body diagram of the ball during impact with the bumper cushion. Identify the n- and t-directions on your FBD.
Step 2: Kinetics (linear impulse/momentum)
Are there forces acting on the ball in the t-direction? If not, linear momentum is conserved in that direction
Are there forces acting on the ball in the n-direction? There is a force, so don't even think about conservation of linear momentum in that direction.
Use the coefficient of restitution to relate the n-components of velocity of the ball before and after impact.
Step 3: Kinematics
Calculate the rebound angle needed for the ball after impact for the ball to be dropped into the corner pocket.
Step 4: Solve
From your equations solve for the angle of incidence for the ball.
Can I treat v_b1 / v_b2 as a variable when solving?
This is how I treated the problem and I was able to get an answer. Hopefully this helps.
Not sure what you are asking. What are v_b1 and v_b2?
In the solve portion of the HW I simplified both of the equations that I got from my kinetics (sum of forces in the t and COR) to have vball1/vball2 (velocity of ball at time 1 and velocity of ball at time 2) on one side. Then I could set the two kinetics equations equal, therefore getting rid of the vball1 and vball2 variables and allowing me to solve for the theta 1. Does this strategy work?
Are we to assume that the velocity of the bumper before and after impact is 0?
Yes, the bumper is fixed.
Yeah I assumed that when I did it.
in this problem is Va1n = Va2n? When I end up working the problem out I get an undefined answer. Using Vb1 = Vb2 = 0 in both directions gets me here as well and im not sure where my mistake is arrising
Sorry, to clarify, A is my ball, and B is the wall in my definition
v_A1n = v_A2n would be true if e = 1, but it's not.
Would the best setup be to set the t-"axis" parallel to the wall and the n "axis" perpendicular to that? Since the FBD is set to the instant of contact, I assumed zero velocity and set-up the path description in that manner.
Yes to: "Would the best setup be to set the t-"axis" parallel to the wall and the n "axis" perpendicular to that?"
Can we use the coefficient of restitution only in the n-direction and not in the t-direction?
Correct.
Why can we not just use trig to find that theta = tan^-1(b/h)?
Because the angles before and after are not equal. The first angle is theta, whereas the second angle has to be taken as a varia le to be solved for. If you take the angle after impact as theta2, you can have theta2 = tan^-1(b/h) and another equation derived using e and including theta, and then equate them to find the angle.
If we are using the equation for coefficient of restitution, one particle would be the ball. are we assuming the other would be the wall, and if so that its v would be 0 at both points due to it being fixed? assuming this would mean e would be fully dependent on the velocity of the ball.
You are correct.