| Problem statement Solution video |
DISCUSSION THREAD
Ask and answer questions here. You learn both ways.
DISCUSSION and HINTS
Recall the following four-step plan outline in the lecture book and discussed in lecture:
Step 1: FBDs
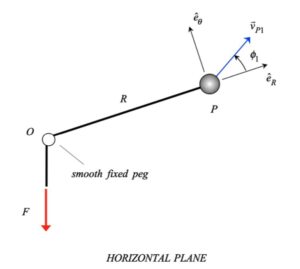
Draw a free body diagram (FBD) of P.
Step 2: Kinetics (Work/energy and linear impulse/momentum)
Since the only force acting on P acts through the fixed point O, there are no moments about O acting on P. Therefore, angular momentum about O is conserved. Note that this equation produces a value for the angular speed ω of the cord, but it does not provide us information on R_dot. Why is that?
Now consider the work/energy equation. There is no change in potential energy. The work done by F is simply F*ΔR. This equation will allow you to solve for the speed of P at the second state.
Step 3: Kinematics
Use the magnitude of the velocity vector to provide the equation that you need to solve for R_dot: v2 = R_dot2 + (Rω)2.
Step 4: Solve
Solve for R_dot, and then write out the vector answer for the velocity of P at the second state.
How are we supposed to find w? I had originally assumed it was 0 but now after reading the hints I'm confused.
Not sure of what you mean by "w". I will respond based on assuming that w is a measure of angular velocity, omega.
For this problem, angular momentum about point O is constant. That is, if you calculate H_O = m*(r_P/O) x (v_P), at the initial and final positions, they will be the same. For the initial position, use the Given information on v_P to calculate H_O. You do not need to find a value for omega.
Does this address your question?
If we don't find angular velocity then how can we use the equation v^2 = R_dot^2 + (Rω)^2?
I believe you can use theta dot instead of omega, which indicates the rate of change of the angle with respect to time, which is just the angular velocity. You should already have theta dot from your LIM equations.
I agree with Merrill, except that theta_dot (or, omega) is found from the angular impulse/momentum equation, and not from LIM (which is probably what Merrill actually meant to say).
you can use angular momentum to find the tangential velocity which is equal to Rw and you can use Work energy to find the magnitude of velocity for position 2. Then you can use the Pythagorean theorem.
Would the work done be negative in this case since F opposes direction of motion?
Yes, the work is negative for the reason stated.
Do we include O in the FBD? Or create a tension force and seperate them?
I think you could do it either way, but I chose to separate them and use a tension force so I could write everything in e_theta and e_r more easily.
If you include the pin O in your FBD, there will be reactions on the pin that act through O. This says that there is no moment about point O.
If you do not include the pin O in your FBD, there will be a reaction force on the rope at point O. Again, with this, there is no moment about point O.
Either way gives the same correct result.
Since it's in a horizontal plane there's no gravitational force right?
We do not have to factor gravitational force into the FBD or our calculations. It's technically still there, though, but there should only be the force from the rope in the FBD.
Yes, since the motion is in the horizontal plane, the gravitational force will be acting perpendicular to that plane. As a result, the gravitational force does not influence the motion of P.
When doing the cross-product for the angular momentum equation are we able to keep the coordinates in terms of etheta and er? or must we translate them to I and j coordinates?
The cross product will produce only a “k” term, regardless of how you write “r” and “v”.
Do I need to find phi2, phi1 is given and my formula is R2*theta_dot = [R1*vp1*sin(phi1)] / [R2*sin(phi2)]? Not sure how to find this.
I am not sure what you mean by your "formula" - where did you find this?
You do not need to actually find phi_2 in order to solve this problem for (R_dot)_2