Chapter 5 Homework

Homework H5.A - Sp 25

9 Comments
Problem statement
Solution video

DISCUSSION THREAD

Ask your questions here. Or, answer questions of others here. Either way, you can learn.

DISCUSSION and HINTS
With the length of cables AC and BD being the same, and with the cables being parallel for all motion, bar AB remains horizontal as it moves. Specifically, ωAB = 0 for ALL time, and therefore αAB = 0 always. (Note that ωAB = 0 does not necessarily say that αAB = 0, only if ωAB = 0 for all time.) Do you see this in the animation?

Since the center of mass for the bar is not equally spaced between points A and B, the tensions in the cables are not the same. You can see this in the animation below.

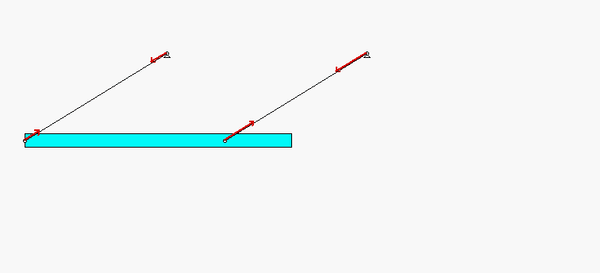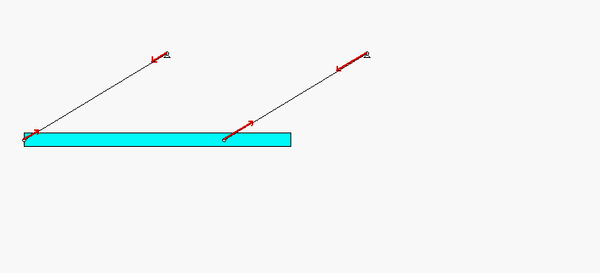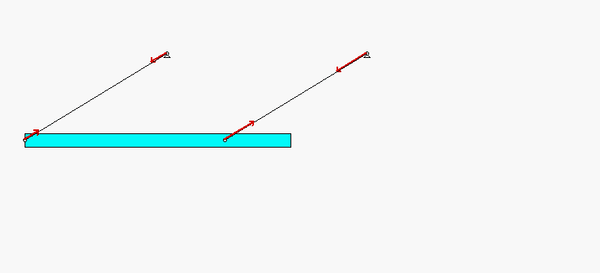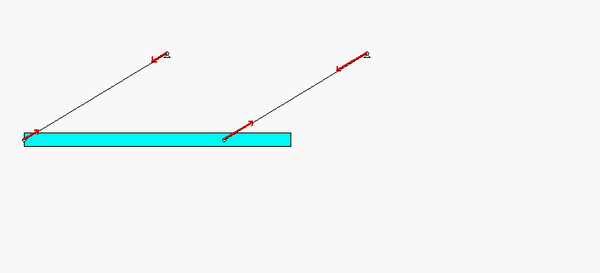
Recall the following four-step plan outline in the lecture book and discussed in lecture:

Step 1: FBDs
Draw a free body diagram (FBD) of the bar.

Step 2: Kinetics (Newton/Euler)
Take care with your Euler (moment) equation. The point about which you write down the moment must be either the center of mass or a fixed point. For example, you can NOT write ΣMA = IAαAB  because A is neither a fixed point nor is it the center of mass.

Step 3: Kinematics
As discussed above, bar AB remains horizontal for all motion. What does the say about the path of the center of mass G of the bar? And, from that, what is the direction of the acceleration of G, aG, at this instant?

Step 4: Solve
From your equations in Steps 2 and 3, solve for the tensions in the two cable. Your equations will contain three unknowns: TAC, TBD and aG.

9 thoughts on “Homework H5.A - Sp 25”

  1. Can we assume the acceleration of g is perpendicular to the force of the two cables? If not, how do we know that direction?

    1. The gravitational force is vertical and downward. The tension forces are at an angle of theta measured from the bar. The vector sum of these three forces is equal to mass times the acceleration vector (which has both vertical and horizontal components)

      1. After using second law I have 3 equations with 4 unknowns Tac, Tbd, aEx,aEy. What kinematic equation can I use to have enough equations to solve?

        1. I believe you can assume that because the bar is moving parallel and A is attached to the end of a string that aG is moving perpendicular to the cables.

        2. Here is the thought process in the Kinematics Step #3:

          * Since AC and BD are always parallel, then bar AB remains horizontal for ALL motion; that is, omega_AB = alpha_AB = 0.

          * If we use the rigid body kinematics equation on bar AB:
          a_G = a_A + alpha_AB x r_G/A - omega_AB^2*r_G/A. Using the above in that equation gives: a_G = a_A.

          * Now consider link AC:
          a_A = a_C + alpha_AC x r_A/C - omega_AC^2*r_A/C = alpha_AC x r_A/C = a_G

          * Since alpha_AC x r_A/C is perpendicular to cable AC, then a_G is also perpendicular to cable AC.

          So, it is not an "assumption" that a_G is perpendicular to cable AC. Instead, it is a consequence of using the kinematics relationships for rigid bodies.

          This is more than just semantics; if you assume such a relationship from the start, you will be wrong in most cases. To see this, go back to the kinematics equation for cable AC. If omega_AC is not zero, then a_G is NOT perpendicular to cable AC. In other words, if the system is already moving, then a_G is NOT perpendicular to cable AC. For an example of this, please see Example 5.A.5 in the lecture book.

          Make sense?

            1. Please follow the steps outlined above.

              All of these problems are such that one ends up with set of N equations in terms of N unknowns. In this case, alpha_AC is just one of the unknowns to be determined from these equations.

  2. Should our final answer be the magnitude of the tension or should it be in vector form?

Comments are closed.