| Problem statement Solution video https://youtu.be/rkIKCA_7Oic |
DISCUSSION THREAD

Ask your questions here. Or, answer questions of others here. Either way, you can learn.
DISCUSSION and HINTS
A cable connects block B to point A on the interior of the disk. We want to know the angular acceleration of the disk on release from rest. Watch the animation of the motion of the disk. What do you see in terms of the relationship between the accelerations of points O and A at the instant of release? And, between the accelerations of points A and B?
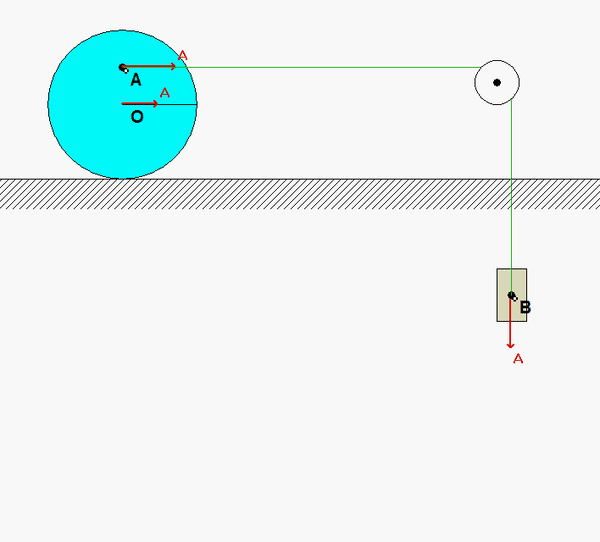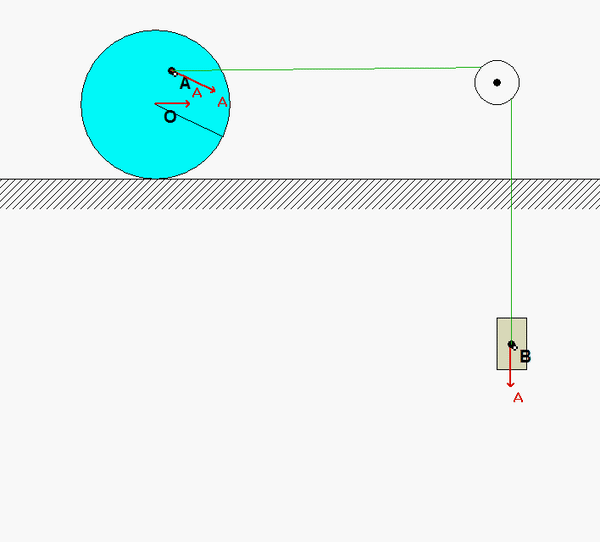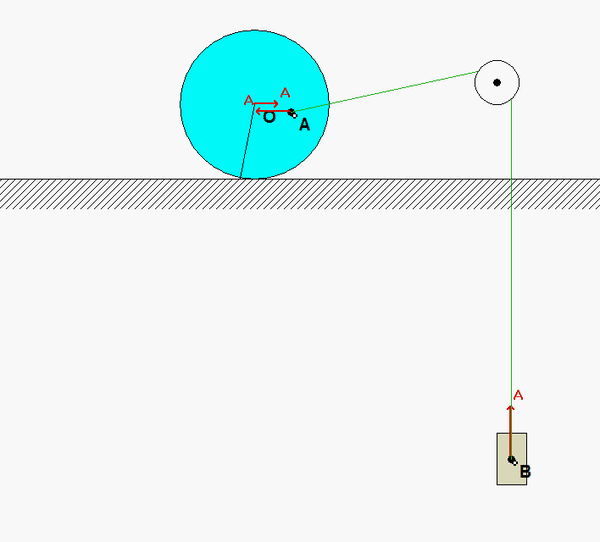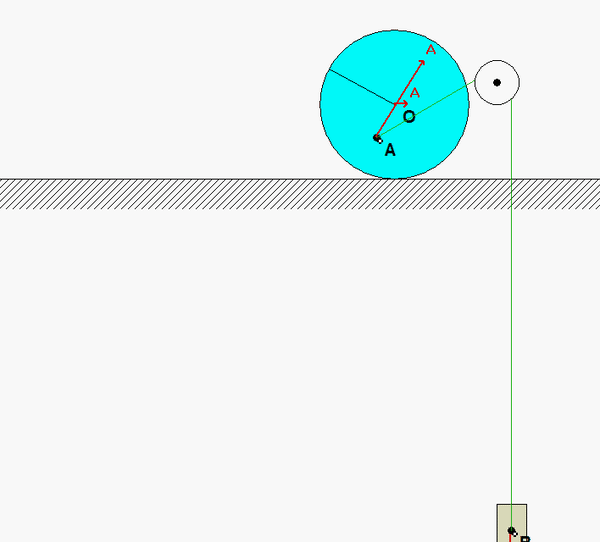
Recall the following four-step plan outline in the lecture book and discussed in lecture:
Step 1: FBDs
Draw individual free body diagrams (FBDs) of the disk and block.
Step 2: Kinetics (Newton/Euler)
Note that the no-slip contact point C will have, at most, an acceleration that points toward O. Because of this, we can use the following Euler equation for the disk: ΣMC = ICαdisk.
Step 3: Kinematics
Since the Newton equation for the block requires us to relate the acceleration of block B to the angular acceleration of the disk through point A on the disk, we should use the following rigid body kinematics equation:
aA= aC + αdisk x rA/C - ωdisk2rA/C
where we know that the horizontal component of acceleration of the no-slip contact point C is zero.
Step 4: Solve
From your equations in Steps 2 and 3, solve for the angular acceleration of the disk.
For the moment equation, why are we taking it at point of contact C instead of O? Wouldn't we want to get rid of the acceleration that is acting on point O for the equation or would we include that acceleration force into our equation if we do the moment at C?
While C is not a "fixed" point like CMK said, it helps me to think of C as fixed. The disk "rotates" around point C since that is the point of contact. By taking the moment around C, it also simplifies unknowns to ones we can find by using known values.
There are 2 main reasons for taking the moment about C instead of O. Although taking it about O would eliminate the rxa component since rG/G=0, you are then forced to include the moment caused by the friction force acting to the left at C. This complicates the problem unnecessarily. If you take it at C, the rxa component becomes 0 because a_C=0 due to no slip. But this time, you don't have to include the moment caused by the friction force because it acts through point C.
Please keep in mind that if you want to use the "short form" of Euler's equation, you need to choose your reference point in that equation as either: 1) the center of mass, 2) a fixed point, or 3) a point whose acceleration vector is perpendicular to the line connecting that point back to the center of mass.
For this problem, C is neither a fixed point nor the center of mass; however, the acceleration of C points directly toward the center of mass O (recall this from rolling without slipping in Chapter 2). Therefore, C is a candidate point for the reference point since r_G/C x a_C = 0.
In short, you are able to use either O or C for the reference point in this problem. Your choice. One advantage of C is that you can avoid dealing with the friction force at C.
This will be discussed in today's class.
For choosing a reference point as you mentioned, the acceleration vector of point C points directly upwards, towards the center of the disk, O. Wouldn't that make the acceleration vector parallel, or co-linear with its displacement vector from point O?
That is correct. The discussion here is that you are able to use either O or C as the reference point.
Is the acceleration of A equal to the acceleration of B to start or do we need to use the rigid body equation to relate aa and ao?
You can find the relationship between the acceleration of A and B by using the inextensibility of the connecting rope.
Because the cable is inextensible, does this mean we can assume that the acceleration at point A is equal to the acceleration of block B?
As far as I understand, the magnitude of the acceleration will stay the same. What you have to be careful with is the sign, which is why doing the inextensible length of rope kinematics is important.
I think you should be able to assume that the magnitude of acceleration of A in the x-direction is equal to the magnitude of acceleration of the block. I believe this only applies to the x-component though, and like Olivia said, make sure you're careful with the sign of your relationship between the two accelerations.
Should we add the direction of gravity to the diagram? I assume that omission was an error.
Almost definitely
The problem says that the disk rolls on a horizontal surface. Therefore all of this motion occurs in a vertical plane.
Is M meant to be smaller than m? Just seems strange but wanted to make sure
That is correct. Larger physical dimensions but made from a less dense material.
When using C as the reference point, would we need to use parallel axis theorem to expand out the expression for moment about C?
I believe you would have to use the P.A.T. because the inertia listed on our notes for a disk is only for the center of mass, so you need to use the parallel axis theorem to adjust, and account for that fact.