| Problem statement Solution video |
DISCUSSION THREAD
Ask your questions here. Or, answer questions of others here. Either way, you can learn.
DISCUSSION and HINTS
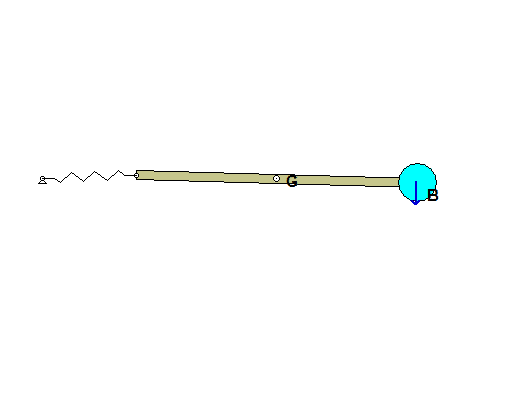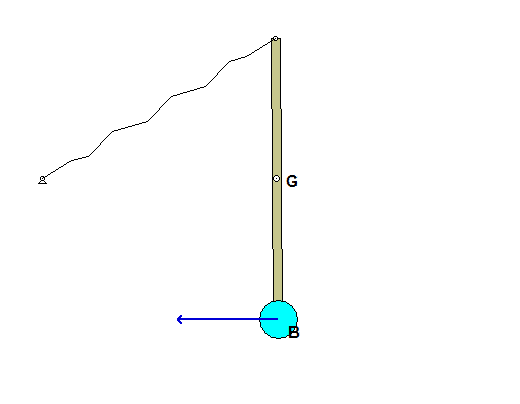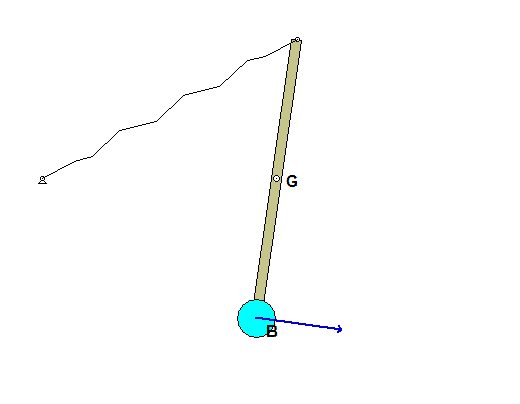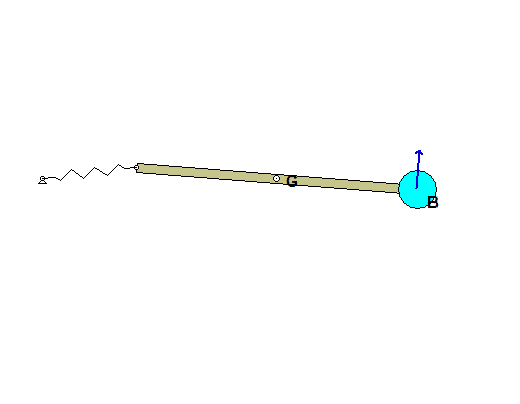
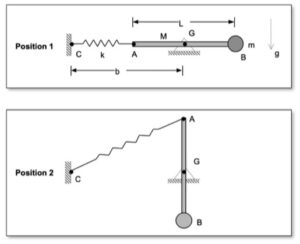
Recall the following four-step plan outline in the lecture book and discussed in lecture:
Step 1: FBDs
Draw a single free body diagram (FBD) of the bar and the particle.
Step 2: Kinetics (Work/energy)
- Looking at your FBD above, which forces, if any, do work that is not a part of the potential energy of the system? If there are none, then energy is conserved.
- Write down the individual contributions to the kinetic energy from the bar and particle, and add together for the total kinetic energy of the system.
- Define your gravitational datum line. Write down the individual contributions to potential energy from the bar, particle and spring, and add together for the total potential energy.
Step 3: Kinematics
Use the following rigid body kinematics equation to relate the angular velocity of the bar to the velocity of the particle B at position 2:
vB= vG + ωAB x rB/G
Step 4: Solve
From your equations in Steps 2 and 3, solve for the angular velocity of the bar.
After calculating angular speed, can we assume the angular velocity is negative because the bar is spinning counterclockwise?
When taking the square root in the final step of your solving for omega, you can take either the "+" or "-" sign. Either one is correct. As you can see from the animation, the "-" angular velocity occurs first. Then, on the return, the "+" angular velocity occurs as the oscillations occur.
We will accept either sign. Good question.
Yes, using the right hand thumb rule, if you follow the movement of the bar you see that the velocity is negative (thumb points into question). So your answer would be in -k term.
When finding the rotational inertia of point G do we use parallel axis theorem to account for the mass at the end of the bar?
Please note the following sentence in Step 2 of the Hints above:
"Write down the individual contributions to the kinetic energy from the bar and particle, and add together for the total kinetic energy of the system."
What this means is to write down the KE for the bar and the particle individually:
T_bar = 0.5*I_G*omega^2
T_particle = 0.5*m*v_B^2
Then the total KE for the bar+particle is:
T_total = T_bar + T_particle.
In Step 3 - Kinematics, you will relate omega to v_B.
Does this help?
yes that makes a lot more sense thank you.
For T_bar you would still use parallel axis theorem though to solve for I_G correct?
I_G for the bar is given by (1/12)*M*L^2. From that you write:
T_bar = 0.5*[(1/12)*M*L^2)*omega^2
For the particle at B:
T_particle = 0.5*m*v_B^2
The P.A.T. is used nowhere here.
I am a little confused on the energy term for this problem. Do we need to take into account both the angular and translational velocities of each point? Since they are only moving rotationally I am unsure wether to use to translational velocity.
Since the bar AB has a fixed center of mass, it will have no translational kinetic energy, only rotational kinetic energy. Particle B can be a little confusing, but since it's a particle, it can't rotate--there's nothing 'inside' it that it could rotate around, so it only has translational kinetic energy. You can relate it's translational velocity to the angular velocity of the bar AB using the rigid body equation in your kinematics step.
Could point A also be a valid place to start with the work/energy equation?
Probably not because it has no considerable mass so what would you write its kinetic energy as in state 2?
There are only two bodies in the problem: bar AB and the particle at B. As discussed above, find the KE for each and add together. A is only a location; it is not a body.
Is there a force between the particle and the bar on the FBDs?
For the system of the bar + the particle, the force is internal, and it does not appear in the FBD.
I'm a little confused as to why step three is necessary. Can we not treat the bar and the particle as one object and just use T = Iw²/2 to find the angular velocity from the energy we calculate?
I think step 3 was useful to determine the exact distance for the nonconservative force in the work-energy equation because it will not just be the given distance times the force because the value found with the kinetics is about the outer edge of the circle and not point O. This way you can see a relation between point O and the outer edge and use this relation to scale your nonconservative force by this relation.
I thought all forces were conservative. The animation shows this. I calculated the work done by the spring using just the change in the length of the spring.
There are sometimes multiple ways to go about solving the problems.
We typically recommend an approach that fits the general solution plan so as to not confuse things. What you describe here will work since the body attached at B is welded to the arm and is a particle; however, if that body were pinned to the bar and had non-negligble dimensions, then that approach does not work.
In short, use speciality approaches with caution. If in doubt, stick with the general plan.
Looking at the variable L, is that distance the length from one end of the bar (A) to the center of the particle or does the particle have a radius as well? I set my datum on the same level as C and am trying to find V2 of the particle, would that then be -(L/2)mg?
Looking at the figure, we see that the distance L goes up till the centre of the particle. Since we only take the centre of gravity of the particle into consideration, we do not need the radius of the particle.
Yes, a part of V2 would indeed be -mg(L/2) with the level of C as the datum as the particle is below C in position 2. However, you also have to consider the potential due to stretching of the spring as a part of V2 using the formula (k delta^2)/2. This will be a positive term.
Also, I believe if the problem says the object should be considered as a particle, that means it is small enough not to have a radius. So as Ayushi said, we do not need to consider if because of the center of gravity, but also simply because it is a particle.
It is a particle by virtue of being a point mass.
If you chose just the bar as the system, would the particle be doing non conservative work on the bar?
I don't believe there is any nonconservative work in this problem if you choose both the bar and the ball as the system. Even if you did only choose the bar as you system, the nonconservative work resulting from the reaction force of the bar on the ball is equal and opposite to the nonconservative work resulting from the force of the ball on the bar (meaning the nonconservative work for the whole system is 0).
Is it possible to only use the parallel axis theorem and treat the bar and particle as one rigid body in the system having one term for the rotational kinetic energy of the bar and particle about G? This would prevent having to include a term for the kinetic energy of the particle alone. Or would this be incorrect and the speed of B has to be added along with the total rotational kinetic energy about G?
It is recommended to keep it simple. Write down the KE of the bar: 0.5*I_G*omega^2. Write down the KE of the particle: 0.5*m*v_B^2. Add these together.