| Problem statement Solution video |
DISCUSSION THREAD
Ask your questions here. Or, answer questions of others here. Either way, you can learn.
DISCUSSION and HINTS
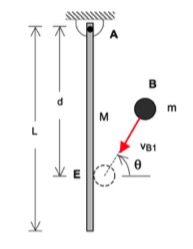
The animation below shows the impact of particle B with the bar.
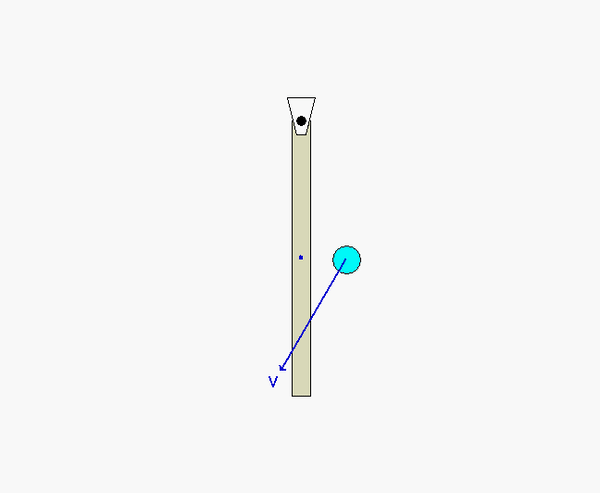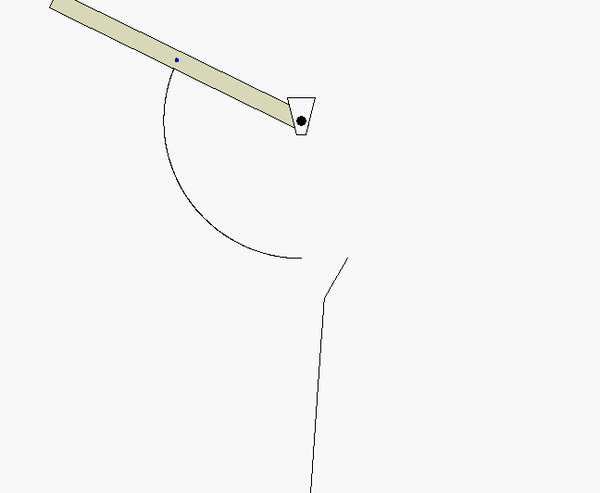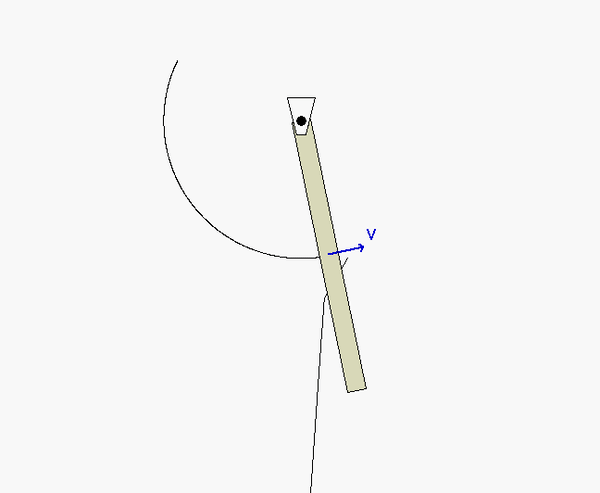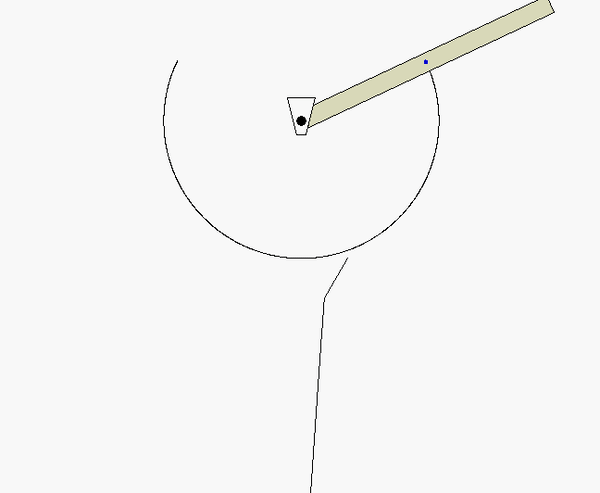
Freeze-frame of motion immediately after impact.

Recall the following four-step plan outline in the lecture book and discussed in lecture:
Step 1: FBDs
Draw a single free body diagram (FBD) of the particle and bar.
Step 2: Kinetics (impulse/momentum equations)
Using your FBD above, sum moments about point A . Consider the time of the impact to be short such that there is no change in position of either the bar or B during impact. Also, consider the particle to be of small physical dimensions.
What does your moment equation above say about the angular momentum of the system about point A?
Step 3: Kinematics
What kinematics do you need to solve this problem?
Step 4: Solve
From your equations in Steps 2 and 3, solve for the angular velocity of the bar immediately after impact.
Would it be acceptable to substitute the variable form of the coefficient of restitution into the angular momentum equation?
Not sure of your question. The COR does not appear in the angular impulse/momentum equation.
If you align your impact axes (normal and tangential) with the axes defined for your system (x and y), you can effectively manipulate your COR, AIM, and kinematic equations to allow you to substitute variables between the three. (Ex. V(b1) in the x-direction being the same as V(b1) in the n-direction)
Would it be appropriate to also look at the linear impulse momentum of just the particle? Since there are only forces acting in the x on the particle?
The particle has the unknown impact force acting on it by the bar. If you write down the LIM equation for the particle, you will need to deal with that impact force.
Recommendation: Do not use this equation. Simply use use the AIM equation for the bar + particle B.
When setting up the coefficient of restitution equation, would you use the velocity of the bar at the center of mass G or at point E, where the particle makes an impact with the bar? Intuitively, I think it would make more sense to use point E because that is where the particle impacts the bar, but the animation included above makes it seem like you should use the center of mass G, instead. Which one is correct?
This needs to be the impact point, E.
Why do you feel that the animation is suggesting G instead?
The animation just shows the velocity of the center of mass of the bar, so that is why I said that.
Oh, OK. We just chose that point as a demonstration of the motion of the bar. It was not intended as a guide in the solution.
Again, use the contact point E.
Since the surface is smooth and the impact is instantaneous, is it safe to say there are no external impulses in the moment equation about A. (We can ignore it)?
When looking at the FBD of the bar by itself, there would be an external impulse on the bar that would appear in the AIM equation.
If you look at the bar + B, then the impact force acting between the bar and B would be internal and would not appear in the AIM equation.
So, it depends on your choice of system.
When you solve for w using AIM and COR, is the answer a scalar? I get a positive value but it should be negative because the bar will rotate CCW?
Since angular velocity is a vector, it is best to present your final answer that way. The vector conveys the "sense" of the rotation, CW or CCW.
For the LIM of the particle, do we use the direction of impact being along theta or only in the x-dir where it collides?
It is best to use the regular "t" and "n" components, just like we did back in Chapter 4. That way you are well positioned to use the COR equation (which employs only the "n" components of velocity).
If you set your coordinate system to the usual n and t components for the impact, we will see that for this impact it is aligned with the global x-y coordinate system, which will then help simplify the coefficient of restitution equation in relation to the other velocities
Do we need to integrate the moment force produced by particle b and include it into our impulse momentum equation?
I think this would depend on what you define as your system. I took both the particle and bar as a system so that momentum is conserved around point A which led to relatively simple calculations.
If this was a perfectly elastic collision could we solve it without using the COR equation?
In a perfectly elastic collision, the COR would be 1. In that case, the solving process should be the same since you can derive an equation for VB2x in terms of e among other variables/givens.
when drawing free body diagram should we include reaction forces at A?
That would be good.
When inputting values into the COR equation, do we plug in scalars or apply our own signs. For example, when plugging in V_BN1, we know it is in the negative x direction, do we plug it in negative so the bottom of the equation becomes -(-vbn1)?
I believe you are correct in what you are saying because to achieve the correct answer vbn1 should be positive in the denominator. Do not forget though that there is an x component to that so it would be multiplied by the cosine of theta.
When assuming that immediately after impact position doesn't change does that mean that we also assume that the angle theta also remains the same right after impact?
The rotation angle of the bar does not change during the short impact time. However, the direction of the velocity of the particle does change during the impact time.
When setting up the coefficient of restitution equation do i use velocity of bar at center or at E, like is the impact with the bar?
The COR equation applies only to the points of contact on each body. This is just like it was back in Chapter 4 when we introduced the impact equations.
When writing our AIM equation, do we use a combination of the particle and rigid body equations? What I mean is using H_B = m*r_B/A x v_B for the particle and H_bar = I_A*omega for the bar such that the right side is (H_B2 + H_bar2) - (H_B1 + H_bar1)
should we use the particle B in the n and t direction or should we covert it into the i and j coordinate plane immediately
Out of curiosity, would this be a case where mechanical energy is conserved? I know the attribute we are supposed to find doesn't have to do with this, but this was asked a lot on exam 2.
Mechanical energy is not conserved since e < 1.
Is it safe to assume Vb2 only has an n component after impact?
Look at an FBD of B during impact. There are not forces acting on it in the "t" direction. Therefore, linear momentum of B in the t direction is conserved. Its t component of velocity is non-zero before impact; it will have the same t component after impact.
For before and after the impact, should we combine the ball and bar into one system? This way we can say that angular momentum is conserved about point A?
Yes, that is the plan recommended in the hints above.
Is it acceptable to utilize the COR to find vb2. Also, is it fair to assume that the particle will bounce in the normal direction?
You can use the COR to find Vb2, but I don't think you can assume the particle will bounce in the normal direction, but I found you don't have to assume a direction because the math will find the direction for you.
The COR equation is to be used to find the "n" component of velocity of B. The "t" component of velocity of B is unchanged by the impact.
How do you combine impulse-momentum and the coefficient of restitution to solve for motion after an impact?
If you write out the impulse-momentum equation you will see that your unknows are omega and Vb2. So you can use the coefficient of restitution to solve for Vb2 in terms of omega and Vb1 (once you include the velocity equation).
Also this will let you solve for omega I don't know if that was your question but that's how I solved this.
How do you go about finding what direction the particle moves in after the collision?
Your math with give you that answer.
When solving for angular momentum is it better to do it about point A or the center of mass of the bar?
That is your call. I recommend point A, however.