| Problem statement Solution video |
DISCUSSION THREAD

Discussion and hints:
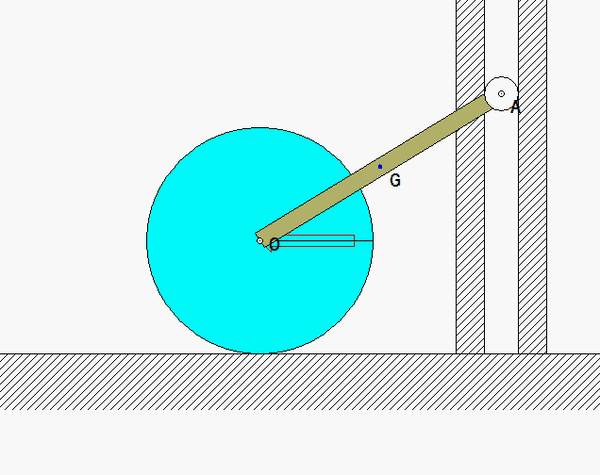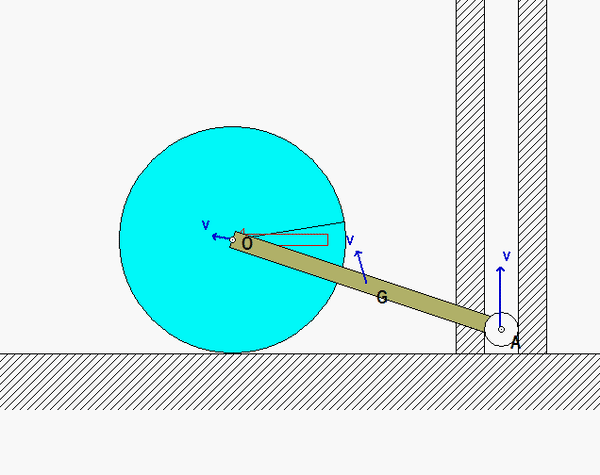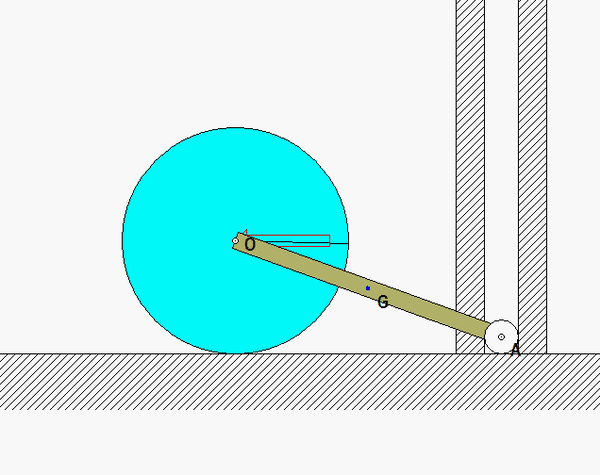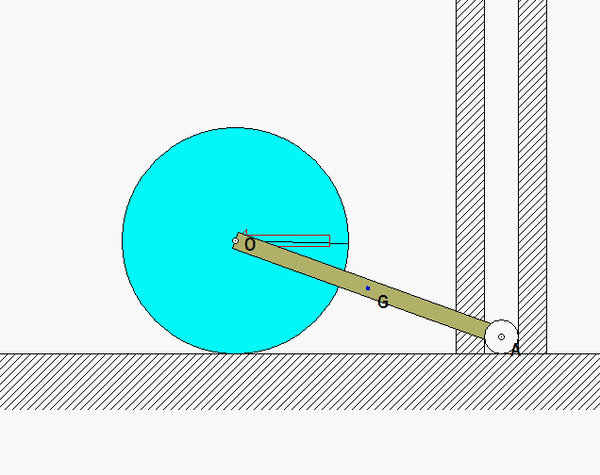
Recall the following four-step plan outline in the lecture book and discussed in lecture:
Step 1: FBDs
Draw a single free body diagram for the system made up of the disk and rod combined.
Step 2: Kinetics (work/energy)
- Write down the kinetic expression for the disk and rod individually, and then add those together to find the total KE for the system of your FBD. For each KE expression, recall that your reference point needs to be either the center of mass of the body, or a fixed point on the rigid body. You might consider using the no-slip, rolling contact point as your reference point for the disk.
- Do the same for the potential energies: write down the PEs for each body individually and add together.
- Also, based on your FBD above, which, if any force, does nonconservative work on the system in your FBD? Determine work for such a force.
Step 3: Kinematics
Note that the instant center (IC) for the disk is the no-slip contact point C. Where is the IC for rod OA at position 2? You might want to review Chapter 2 of the lecture book in finding the IC for a rigid body moving in a plane. (Carefully study either the animation above for position 2 or the freeze frame for that position below – you can actually see the IC from these!) Locating this IC is critical for you in setting up and using the kinematics for this problem.

Step 4: Solve
Solve your equations above for the velocity of point A.
Any questions?
From this free frame, it looks like the velocities of G and A are parallel, wouldn’t this imply that there is no Instant center for the bar and that the motion for the bar at this point is purely transnational?
The IC for OA is at the intersection of the perpendiculars to the velocities of O and A. This intersection is at O.
Points on a rigid body with parallel velocities with the corresponding perpendiculars that lay on top of each other does not say pure translation.
I’m getting confused at how the IC is at O. The velocity of O is horizontal while the velocity of A is vertical, the intersection of their perpendiculars should be above O but not exactly on O. I don’t know if I’m confusing something.
At this freeze frame, if O has a horizontal velocity, and A has a vertical velocity, the intersection of their perpendicular lines would meet exactly at point O, with v_a’s perpendicular going along the beam AO. It may help to draw out the perpendiculars at this instant to help visualize the situation. Hope this helps!
Since point O is not able to translate up and down this means that there must be a IC since G and A are moving downward and O is not. This can be seen in kinematics relating the velocity of point O and point G or A.
One thing that can make it easier to visualize the IC of the bar is that it is always on the same vertical axis as O since it moves horizontally and on the same horizontal axis as A because it moves vertically. This means that at position 2 it is directly on O.
You’re right to question that — if O has a horizontal velocity and A has a vertical one, their perpendiculars would intersect above O, not at it. But if the IC is at O, that means O is instantaneously at rest, and the whole body is rotating about that point — so O wouldn’t have any velocity in that case.
I am unsure about the doubts expressed here on the location of the IC for the bar. The IC for the bar at position 2 is exactly at point O. For instants in time before position 2 the IC is ABOVE O.
Do we need to account for the velocity of the disk at all in this problem since it is released from rest and is at an instant at rest when at state 2?
It appears not.
You would not need to account for any initial velocity but the energy of the disk can still be in the form of its rotational velocity which I also got to be zero at state 2. As a result, I did not use any velocity of the disk and that seemed to work just fine.
Would it be the most beneficial to choose the datum when theta=0 since this would help eliminate the potential energy term at state 2? Or is there a better way?
I do not see any particular advantages of where you place the datum line for gravity.
It doesn’t matter where the datum goes as it will be either positive on one side of the equation (above datum) or negative on the other side (below datum). Both yield the same result in this case.
You can place the datum for a question with gravity anywhere you want since everything will balance out. Ideally, if you place the datum at the center of mass of an object that does NOT change elevation, that object never needs to be considered within the gravitational potential.
It would not matter where you place it because the disk does not move up or down. If you make your datum at state 2 then the term will show up in state 1 and visa versa for the bar.
An interesting question emerged when discussing this problem with a fellow student, and I thought I would share our findings for any other curious people. It’s advantageous to take kinetic energy of the bar about O, since it’s an instant center and thus only has rotational kinetic energy. In contrast, if kinetic energy is taken about the center of mass, there is both rotational and translational kinetic energy that needs to be accounted for. The question emerged, if the kinetic energy was taken about point A, would it not have both the same rotational energy as the bar about O, in addition to translational energy? This suggests that the kinetic energy evaluated about both points yield different answers. What we discovered was that, since A is neither a fixed point nor the center of mass, the 3rd term in the kinetic energy equation, ω*V_p*(ω x r_G/P), doesn’t drop out and must be accounted for. It’s this term that reconciles the kinetic energy equations about points O and A, and demonstrates in a way why the term must be present in the equation.
this is interesting could you then explain why If kinetic energy is frame-dependent, why is the total energy conserved in all inertial frames?
I will let Simon respond to this. In the meantime, it is my opinion thar he is not referring to different reference frames. Instead, he is referring to the choice of reference points that are used to express KE.
Would the velocity in the disk throughout the whole problem be zero since it begins at rest and the disk changes direction when theta equals 0
The disk does have velocity and angular velocity (because it rolls without slip). For work-energy, we only look at the initial and the final state, which in this case means 0 initial/final velocity. What happens between your initial and final state doesn’t matter.
How we know the disk has 0 final velocity?
Locate the IC for bar OA. See the freeze frame of the motion above at the final state.
We know that the disk has a final velocity of 0 because at theta=0 it is changing direction, which you can see in the animation. Therefore, it has both a velocity of 0 in the x direction, and an angular velocity of 0.
How should we show the velocity of point o is zero other than it the instant center-or is that enough to show that we know–and can call w 0?
In Step 3, make a drawing of the system at position 2. Show the construction lines needed for finding the IC, and write down the location of the IC. Use that result in your analysis.
Would the applied force F be the only non-conservative work force or is the friction force also included in this?
The friction force does not do work, as it is located at a no slip contact point. This point has no velocity, meaning that it is technically stationary and no work can be done at the point.
This is quite a counter-intuitive idea at first, but I ended up finding a visual that helps. If the wheel and no slip surface was replaced with a gear on a rack, then instead of friction acting at the contact point, a normal force would. This normal force acting in the same direction as the original friction force did would not be doing any work, as the displacement would be zero.
Can we neglect the moment due to the normal force at the point of contact with the surface?
This is a W/E problem, not N/E.
I’m having trouble finding the distance that defines the work done by force F on the system. How would I go about finding this?
I found it best to think about it in terms of how far the bar travels or what the start of the bar is and where the end of the bar is. In a way I used a W/E problem statement where I compared state 2 of the bar length in the x direction to state 1.
At state 2 would the angular velocities of the bar and disk be equal? if not, how would we relate the two?
The two angular velocities are not the same. Recall that O is the IC of the bar making the velocity of O to be zero. Since the disk rotates about the no slip point, then the angular velocity of the disk is zero.
Why do we use the moment of inertia about point A for the rod? will it be the same thing to do it for point A or point O for the rod?
Recall that in order to use the “short form” of the KE expression, you need to choose the reference point to be either: the center of mass OR a fixed point. Since A is neither, you cannot use A has the reference point.
In this problem, however, you can use point O since it is the IC for the bar. It turns out that the mass moment of inertia of the bar about O is the same as the mass moment of inertia of the bar about A. It is this reason that you can use I_A in the KE expression.
At theta = 0 would the kinetic energy be equal to 0?
No, because both of these forces do positive work, causing the system to accelerate as it rotates and moves. So by the time it reaches theta = 0, it’s gained kinetic energy.
At theta = 0 or state 2 the kinetic energy would not be equal to 0. The bar is still having a rotational energy since it continues to move, we just choose to look at the freeze-frame instant.
Would it matter where you take the kinetic energy for the disk? If so, how would this make the problem different?
It would not matter so much where you take the kinetic energy of the disk, what matters is the point of rotation you pick for the disk and bar as it what change your moment of inertia.
Do you need to use the parallel axis theorem to find the Io of the bar in the kinetic energy equation for the bar? Or is Io just 1/2mL^2 with no additions
To find Io of the bar, yes, you would need to use parallel axis theorem.
1/2mL^2 with no additions is the moment of inertia around the bars center of mass.
The subscript on I_O means something. The subscript says that you need to mass moment of inertia about point O. Mass moments of inertia are typically provided in terms of being about the body’s center of mass G.
* If O is the center of mass, then I_O = I_G
* If O is not the center of mass, then you need to use the PAT to find it:
I_O = I_G + m*d^2
where d is the distance between O and G.
Does that make sense?