| Problem statement Solution video |
NOTE: The original posting of this problem had the wrong units on r and vP. These parameters should have units of m and m/s, respectively, as currently posted in the problem statement.
DISCUSSION THREAD
Discussion and hints:
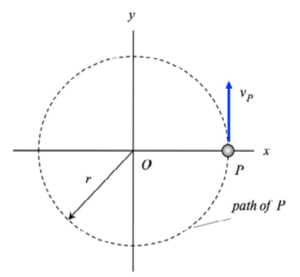
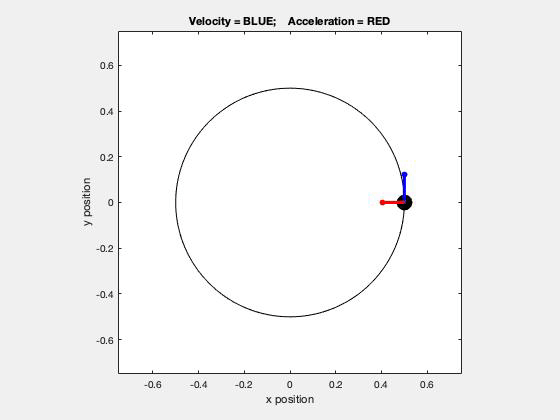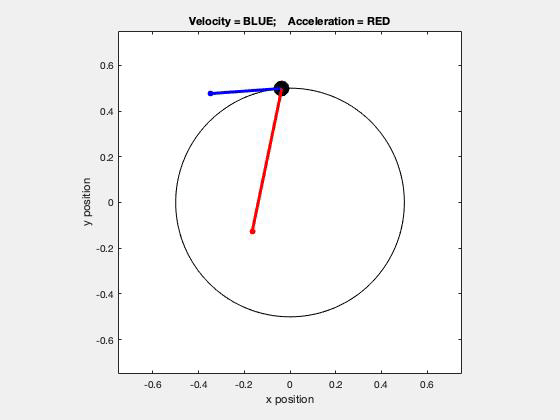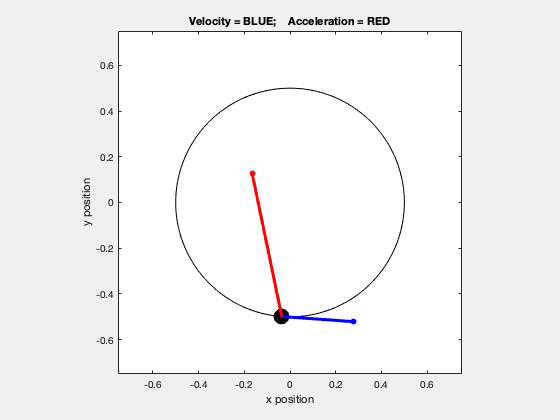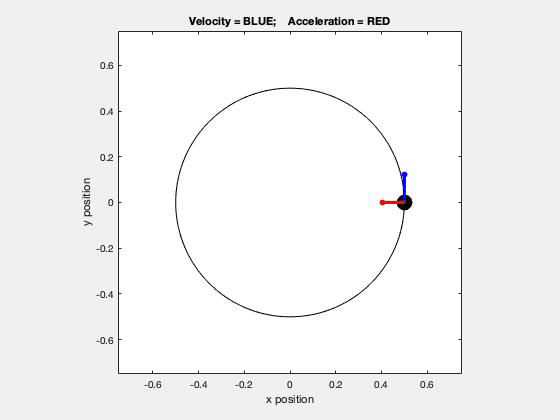
Using the path description, we know that there are two components of the acceleration vector: one that is tangent to the path (the rate of change of speed), and one that is normal to the path and pointing inward toward the center of curvature (the centripetal component). The tangential component of acceleration will point:
- in the direction of motion if the speed is increasing,
- in the opposite direction of motion if the speed is decreasing, and
- will be zero if the speed is constant.
All three situations are shown in the above animation - are you able to see these?
We encourage you to interact with your colleagues here on conversations about this homework problem.
When is this homework due?
This homework is due this Friday, along with homework H.1.D. The syllabus recently got updated with a course calendar on the very last page.
How complex should the drawing for the 3 cases be?
I do not believe the drawings need to be complex. I think it should just be obvious what you are trying to show and labeled correctly. As stated in the hints the motion of the vectors is dependant on whether it is increasing or decreasing or no movement at all, so based on that the direction of the vector is chosen and then can be shown on a simple diagram as drawn in the problem itself.
Is it okay to use the path coordinates for the calculations and then convert to cartesian coordinates?
Do as you suggest - convert to Cartesian once you have found them in path. Be sure to show the path unit vectors in your sketches.
Since the path is a circle is rho just equal to the radius?
Yes, that is correct.
e_t is a unit vector that should always point tangent to the path and in the same direction as velocity, correct? But the tangential component of the acceleration can point in opposing direction of the velocity, while still being tangent to the path?
Yes, e_t always points in the same direction as the velocity.
For acceleration, we know that the tangential component of acceleration is the "rate of change of speed". Therefore:
* If the tangental component of acceleration is positive (that is, pointing in the positive e_t direction), then the rate of change of speed is positive. From this, we say that the speed is INCREASING.
* If the tangental component of acceleration is negative, then the rate of change of speed is negative. From this, we say that the speed is DECREASING.
Does that make sense?
Yes indeed! Just wanted to make sure I had it straight before causing issues later. Thank you!