DISCUSSION

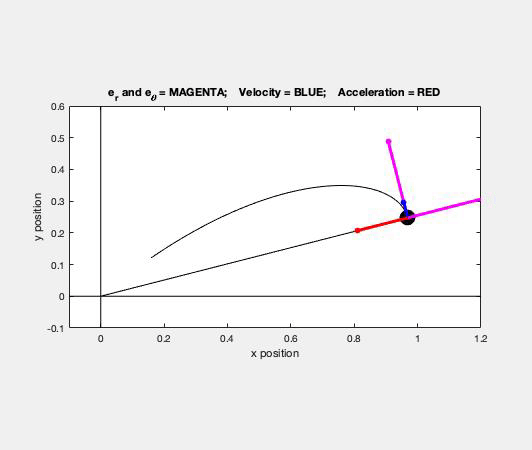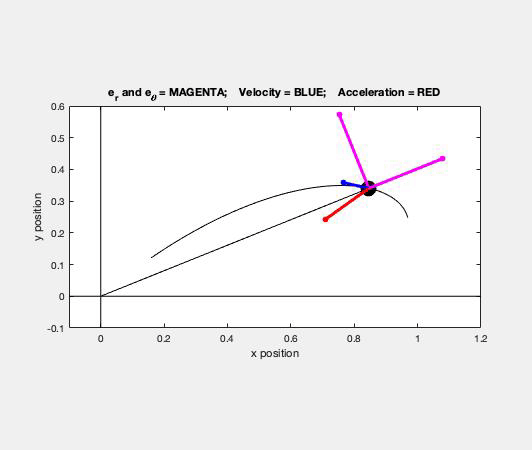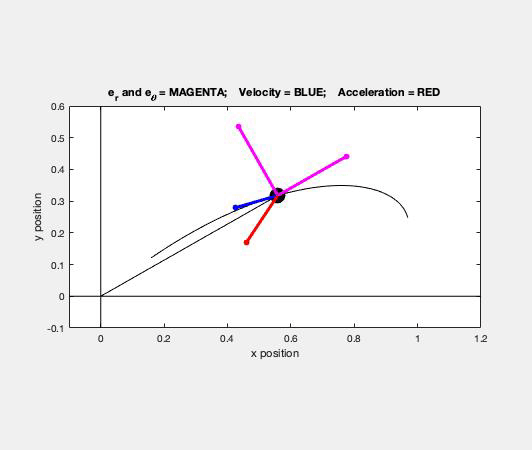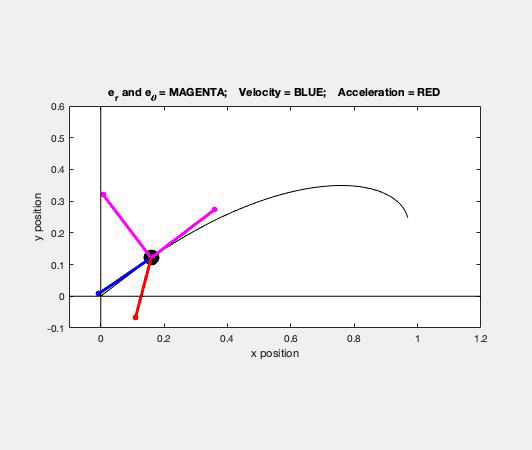
As you watch particle P move through its path, focus on a few things:

• Direction of the velocity vector. The velocity of the ball is always tangent to the path, as expected. Note that the unit tangent vector e_t points in the same direction as the velocity.
• Direction of the acceleration vector. The acceleration of the P always points "inward" on the path, again, as expected. Here you see that the acceleration vector points in the positive e_t direction; therefore, its speed must be increasing with time (as it is).
• Directions of the polar unit vectors. The e_r unit vector always points outward from  point O toward P. The e_θ unit vector is perpendicular to e_r, and in the direction of increasing θ, as seen in the animation above.

Your task is to calculate R and θ, and their time derivatives. Here, you are given R and θ explicitly as a function of time. Therefore, the chain rule of differentiation is not needed.

Any questions?? Please ask/answer questions regarding this homework problem through the "Leave a Comment" link above.