Chapter 2 Homework

Homework H2.J - Fa24

6 Comments
Problem statement
Solution video

DISCUSSION THREAD

Any questions??

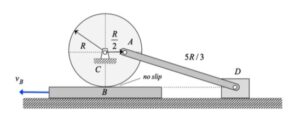
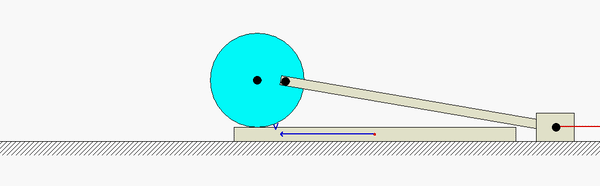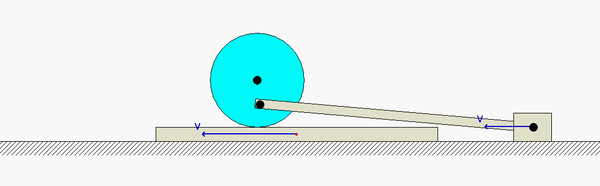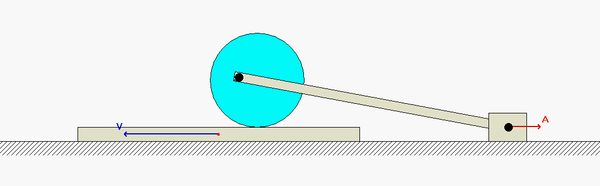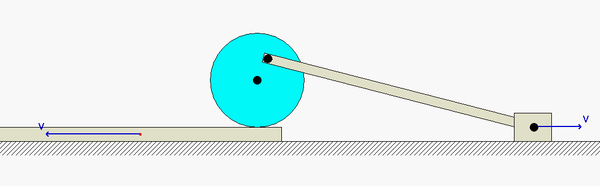
Before starting this problem, make note of the type of motion for each component in the mechanism:

  • Block B is in pure translation, and moves to the left with a constant speed of vB.
  • The disk is pinned to ground at its center C and moves in pure rotation; that is, C is the center of rotation of the disk. Because of this, the velocity of A is in the vertical direction.
  • Slider D is in pure translation, and, at the instant of interest, D moves in the same direction as does Block B.
  • Link AB has both translational and rotation components of motion.

Question: Where is the location of the instant center (IC) of AD at this instant? Reflect back on the observations above in answering this. You can use the location of the IC for AB to either find the angular velocity of AD, or to check your answer found from vector analysis.

HINTS:

  • Use the rigid body kinematics equations relating the motion of the contact point on the disk (call that point E) to the center C of the disk to find the angular velocity and angular acceleration of the disk:
    vE = vC + ωdisk x rE/C
    aE = aC + αdisk x rE/C - ωdisk2 rE/C 
  • Use the rigid body kinematics equations relating the motion of points A and B to find the angular velocity and angular acceleration of the link AD:
    vD = vA + ωAD x rD/A
    aD = aA + αAD x rD/A - ωAD2 rD/A 

Shown below is a freeze-frame capture of the animation of the motion for this mechanism at the position of interest (when link AC is horizontal). Note that the velocity of D is to the RIGHT at this position. The direction of motion quickly changes to the LEFT at the point where D becomes the IC of AD, as it should.

6 thoughts on “Homework H2.J - Fa24”

  2. When point on the disk is in line with the center (either horizontally or vertically), then the velocity in the that direction is neither increasing nor decreasing, correct? So the acceleration of point A should have only a horizontal component and the acceleration of point B should have only a vertical component, right? Similarly, since point E on the disk is touching block B, should the velocity of E be the same as the velocity of the block? Or is there something I am missing that allows for the calculations to be completed without these assumptions?

    1. Yes, point A will have only a horizontal component of acceleration.

      Block B is moving in the horizontal direction with a constant speed. Therefore, B has zero acceleration.

      Yes, the velocity of the contact point E on the disk will have the same velocity as block B.

  3. I'm having a hard time finding the accelerations since I get down to only two equations with three unknowns (aD, α, αAD) can someone explain the rough set up to be able to have enough information to find the angular acclerations?

    1. I did mine using point B to find angular velocity of the disk and then center of disk to find acceleration of A. for AD you can try to use IC method to find angular velocity of AD. Now you have everything to find Ad and acceleration. Also, acceleration for D only in one direction, so one part equal to 0, and second to a_d. That will be helpfull at the end

Leave a Reply