| Problem statement Solution video |
DISCUSSION THREAD
Any questions?? Please ask/answer questions regarding this homework problem through the "Leave a Comment" link above.
Discussion
.
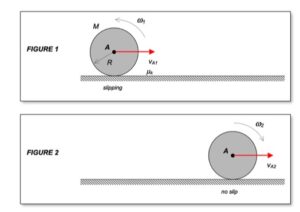
The animation shown above demonstrates the relationship between the translation velocity of the disk's center A and the angular velocity of the disk. Recall that the disk is initially projected to the right with an initial velocity of A and a counterclockwise rotation rate; that is, the disk is given a "backspin" on release.
As the disk slides, the friction with the floor does two things: it slows down the translational motion of the disk, and exerts a clockwise moment on the disk reducing the rotational rate of the disk. At some point the rotation rate changes from counterclockwise (positive) to clockwise (negative). And shortly after that, slipping ceases to exist between the disk and the floor. Rolling without slipping starts at the point where the plots of velocity of A and angular velocity of the disk go "flat".
HINT: As always, we should follow the four-step plan for solving this problem.
STEP 1: FBD. Here, draw a free body diagram of the disk.
STEP 2: Kinetics (here, linear and angular impulse momentum equations).
STEP 3: Kinematics. Slipping ceases when the velocity of the contact point on the disk with the ground goes to zero. At that point: vA = ω x rA/C, where C is the point on the disk in contact with the ground.
STEP 4: Solve
Is it true that the force of friction exists for figure one and figure two, except in figure one the fricition is kinetic and in figure two the friction is static? Should we draw seperate free body diagrams?
As static friction isn’t given in the problem, I’m assuming that we don’t have to worry about it. I believe that static friction doesn’t do any work because there isn’t displacement at the contact point when no slipping occurs. Meanwhile there is displacement occurring when the slipping condition occurs.
Correct conclusion.
The force of friction is the only external force acting on the rigid body, correct? So the left hand side of the angle impulse equation would only have Frictional force * R in the integral?
Correct - friction is the only force acting on the body in the direction of travel. Note that the moment due to friction is in the negative z-direction.