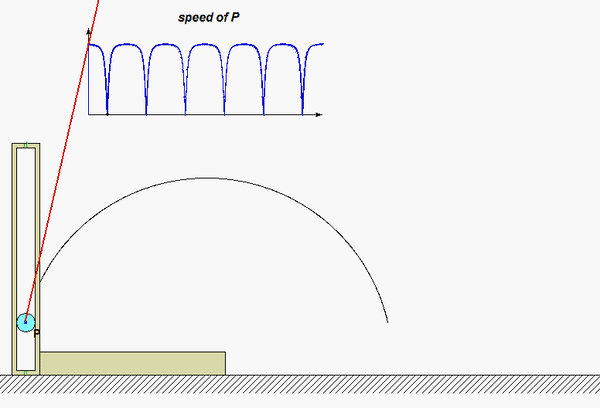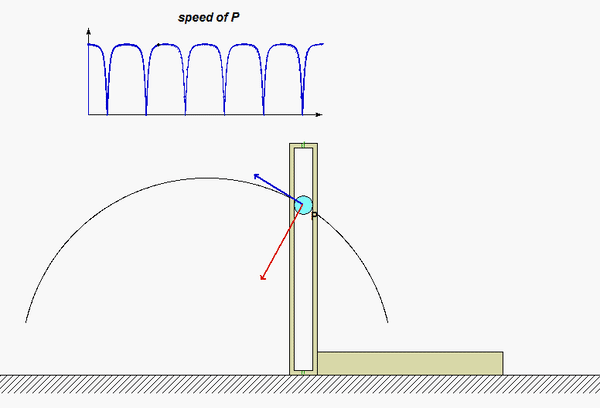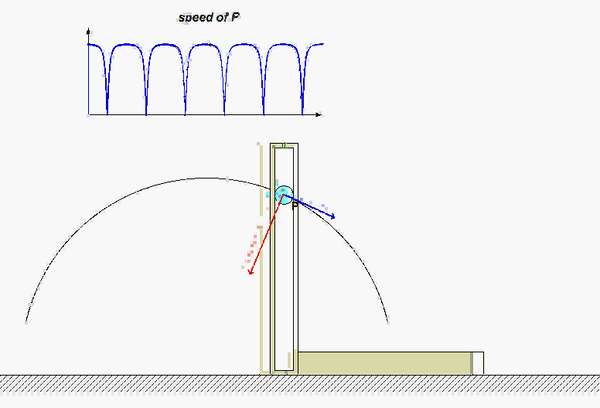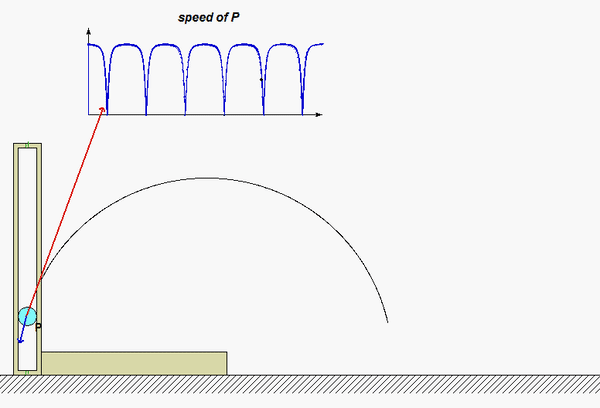
| Problem statement Solution video |
DISCUSSION THREAD

Discussion and hints:
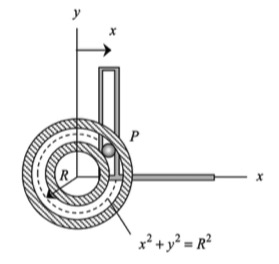
In this problem, one simply needs to differentiate both the x- and y-coordinates once with respect to time in order to find the corresponding Cartesian components of velocity. Taking another time derivative of each then produces the Cartesian components of acceleration.
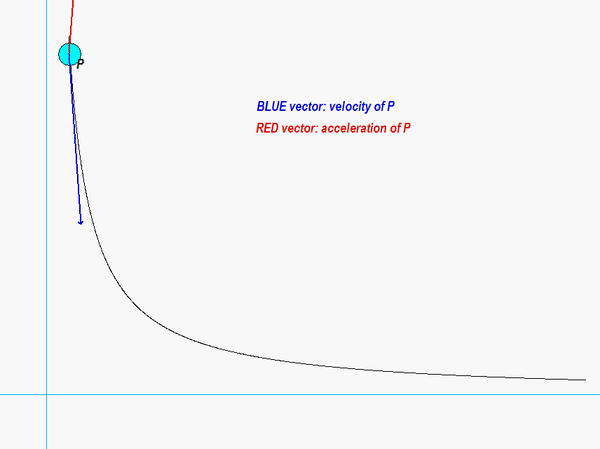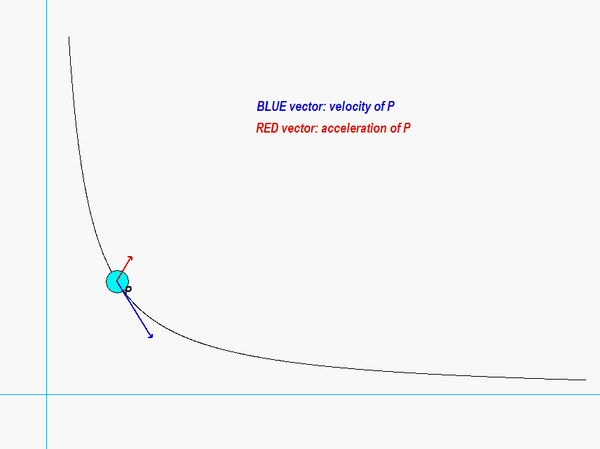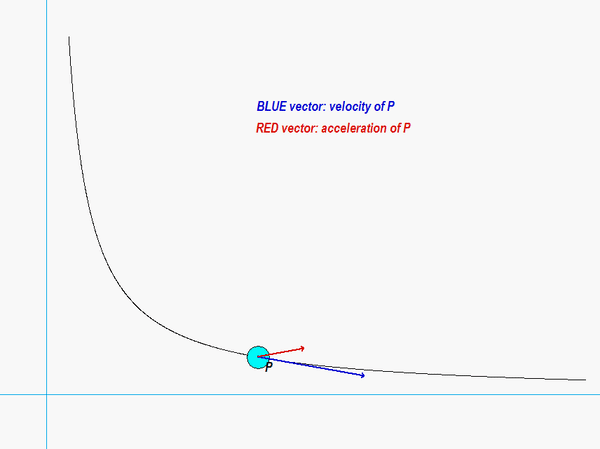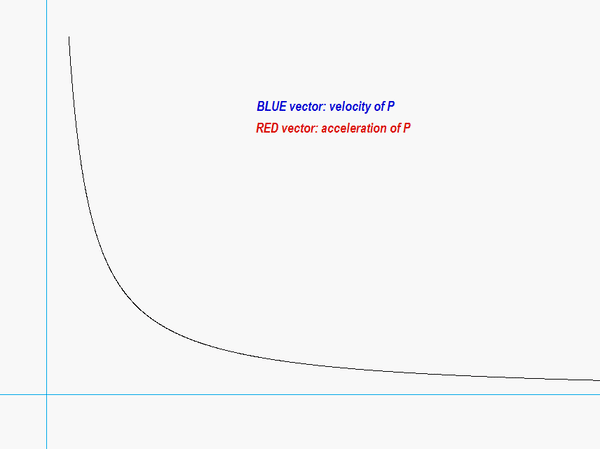
The results of this analysis are shown in the animation below. From this animation, we see that the velocity of the P (shown in BLUE) is always tangent to the path of P. The acceleration (shown in RED) is not quite so simple: it has components both tangent and perpendicular to the path; however, the component perpendicular to the path always points inward on the path. Both of these observations are consistent with what we see in the next lecture when we develop the expressions for velocity and acceleration in terms of their PATH components.
Any questions??