Ask and answer questions here. You learn both ways.
DISCUSSION and HINTS
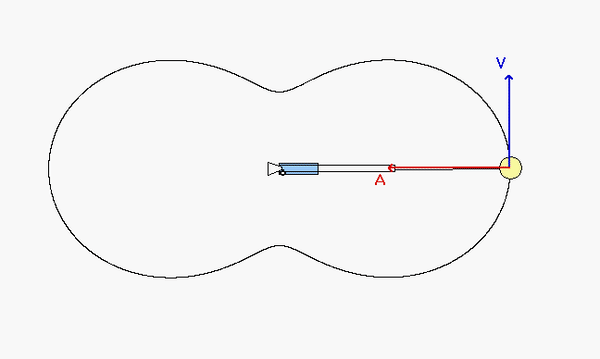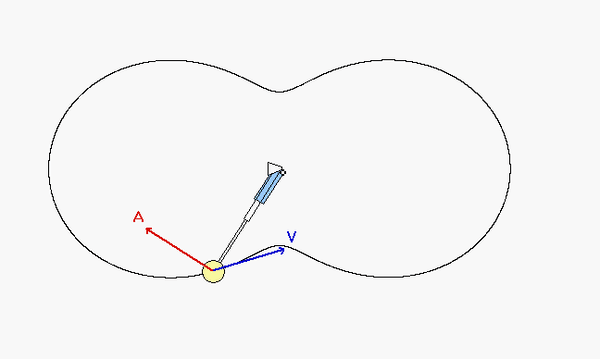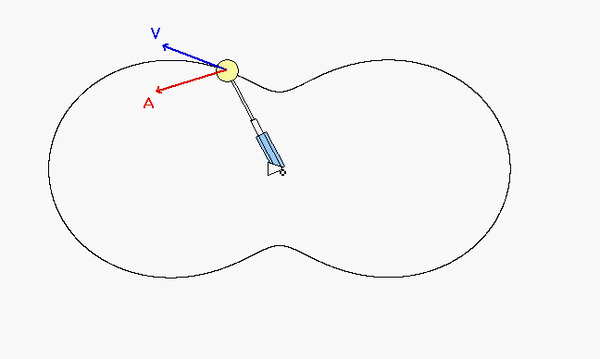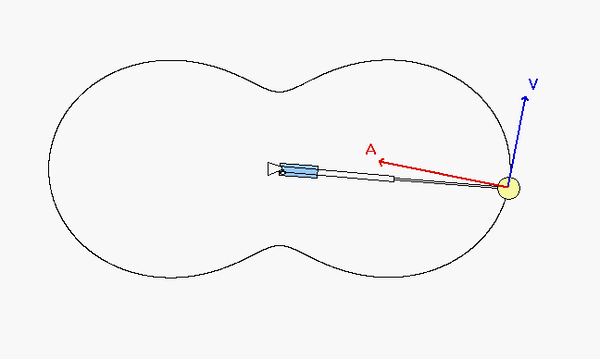
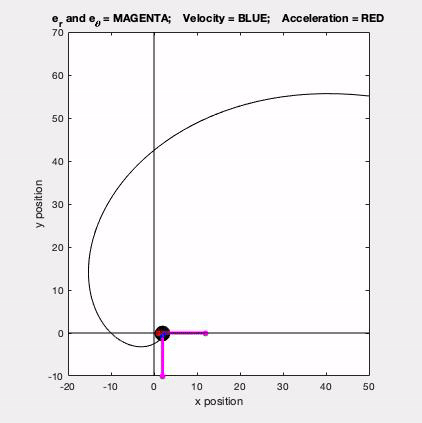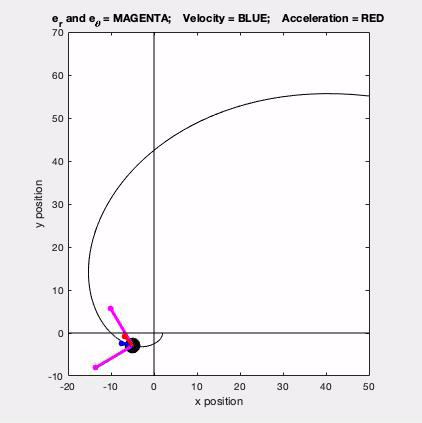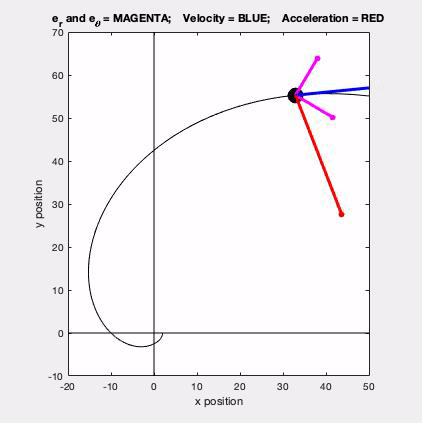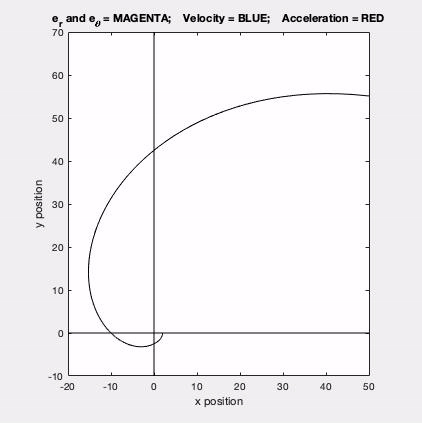
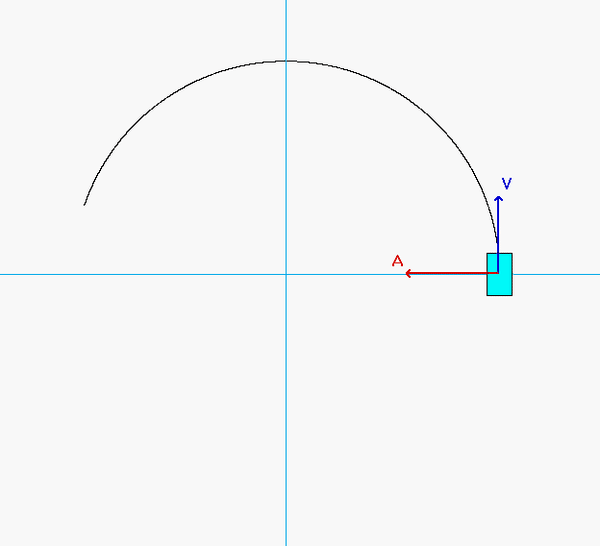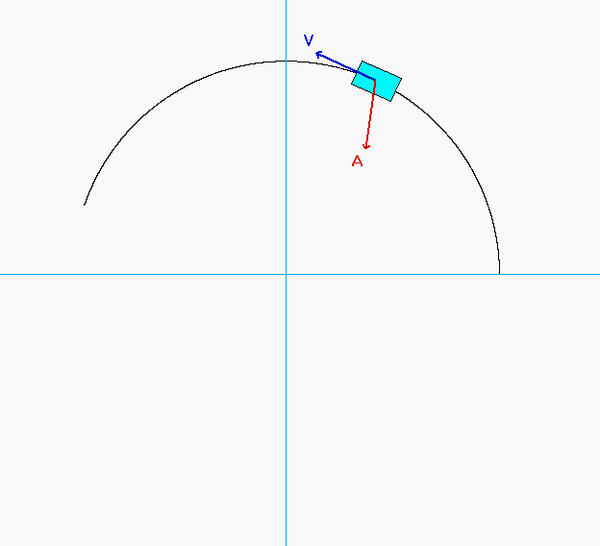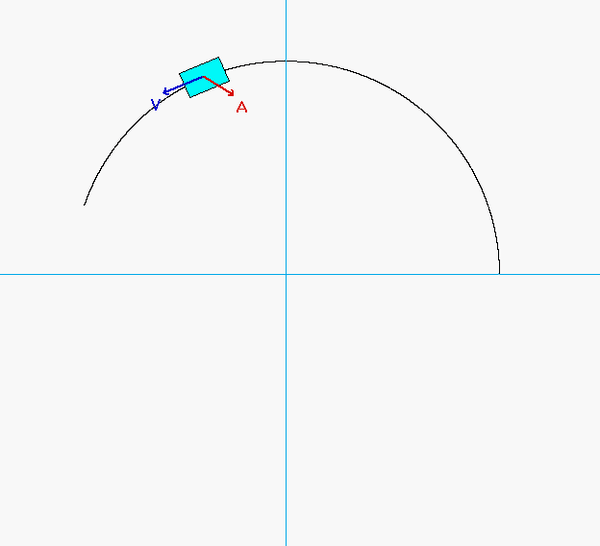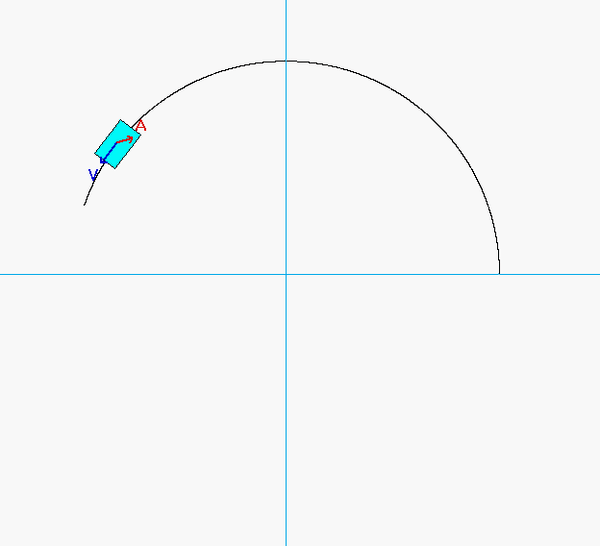
As expected, the acceleration of P has both non-zero tangential and normal components.
- From the equation provided for speed as a function of distance traveled, the speed of P is monotonically increasing over time. Therefore, the tangential component of acceleration always points "forward" of the direction of motion.
- Although the speed of P is increasing, the normal component appears to decrease as P moves along its path - why is that?
Can you see these two things in the animation below?
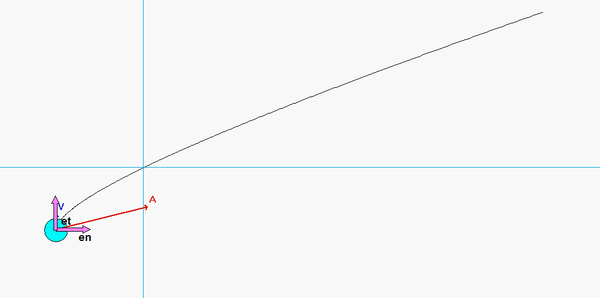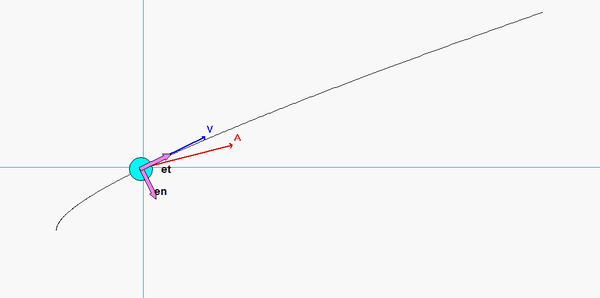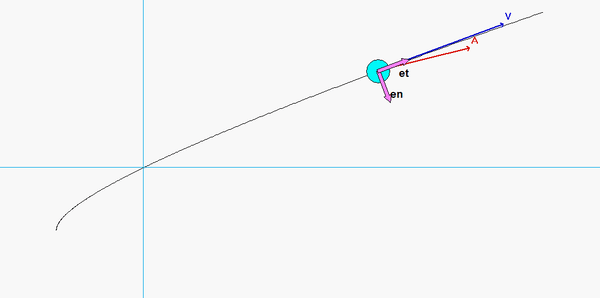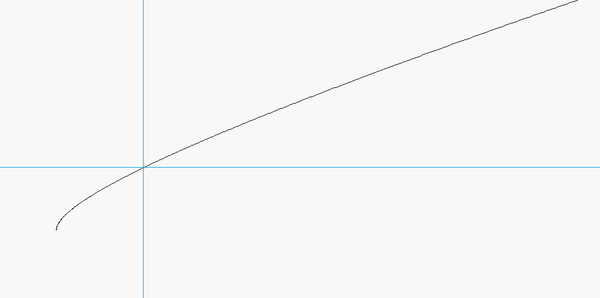
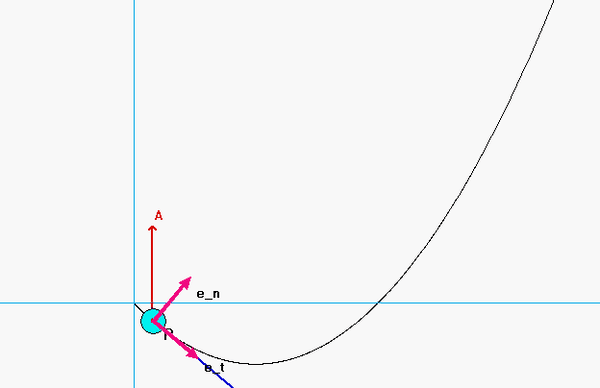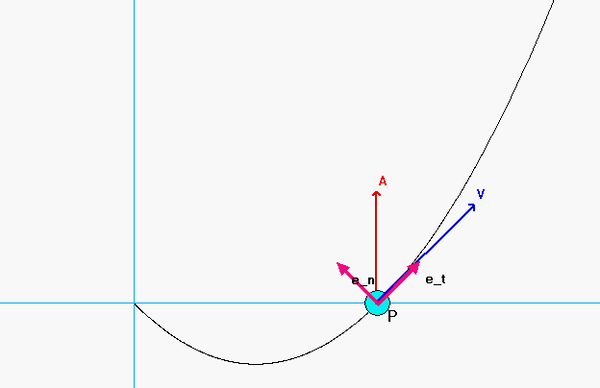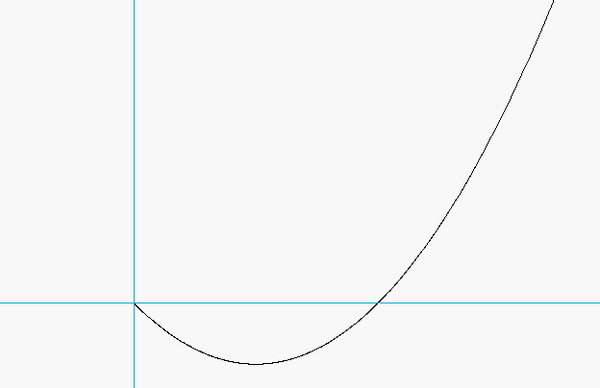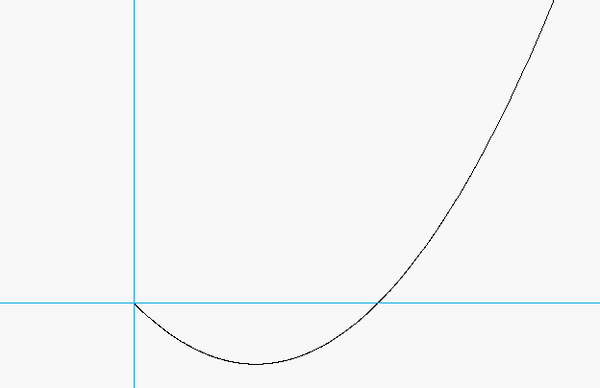
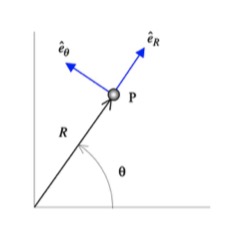
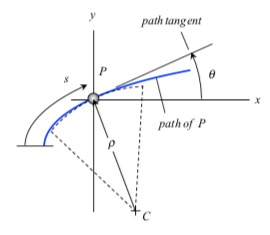
Recall that the general path description velocity and acceleration equations are given by the following:
v = v*et
a = v_dot*et + (v2/ρ)*en
Part (b)
Note that v_dot = dv/dt. For this problem, we do NOT know the speed as a function of time; instead, we know speed as a function of position, s. To find v_dot, we need to use the chain rule of differentiation: dv/dt = (dv/ds)*(ds/dt) = v*(dv/ds).
Part (c)
Use your sketch in Part (a) to write et and en in terms of i and j. Substitute these in your results from Part (b) to find the x- and y-components of velocity and acceleration.
Part (d)
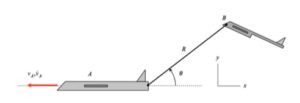
The center of curvature of the path, C, is located in the en direction at a distance of ρ from P.