Any questions??

DISCUSSION
In some sense, this is a very standard kinematics of rigid bodies problem. A rigid link connects points A and B. To relate the motion of these two points, you will need the following kinematics equations:

v_A = v_B + ω x r_A/B 
a_A = a_B + α x r_A/B – ω² r_A/B

The nuance in this problem is the acceleration of point A. From what we learned earlier in the semester, the acceleration of a point can be written in terms of its path coordinates; that is, here the acceleration of A can be resolved into its tangential and normal components. As you proceed on this problem, you first need to recognize the tangential and normal unit vectors, e_t and e_n, for the motion of A. Then write down the acceleration of A, first in its path components, and then in its Cartesian component. In the end, you will have two scalar equations coming from the rigid body acceleration equation in terms of two unknowns.

Ask and answer questions here. Help others with thoughtful responses to their questions. You will learn from the experience.

DISCUSSION and HINTS
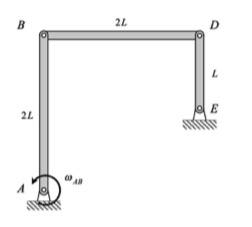
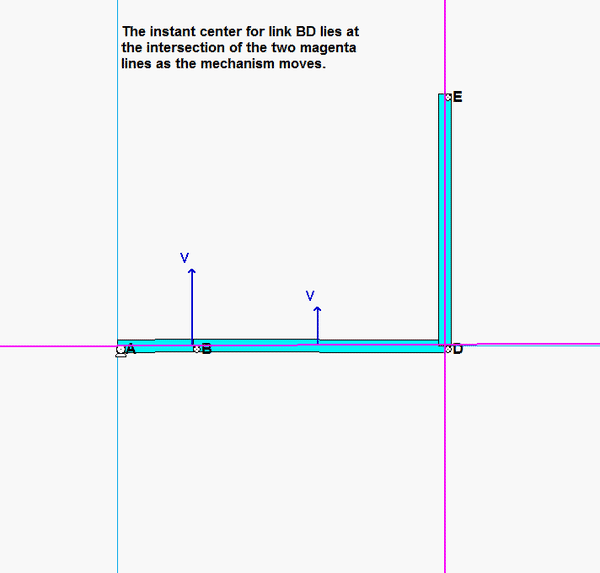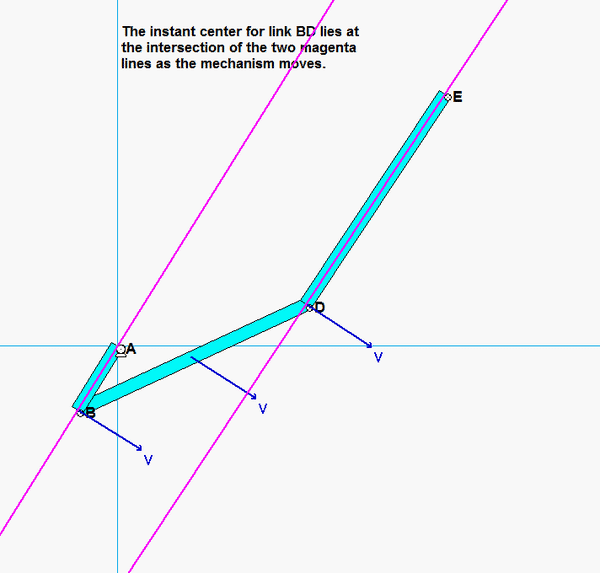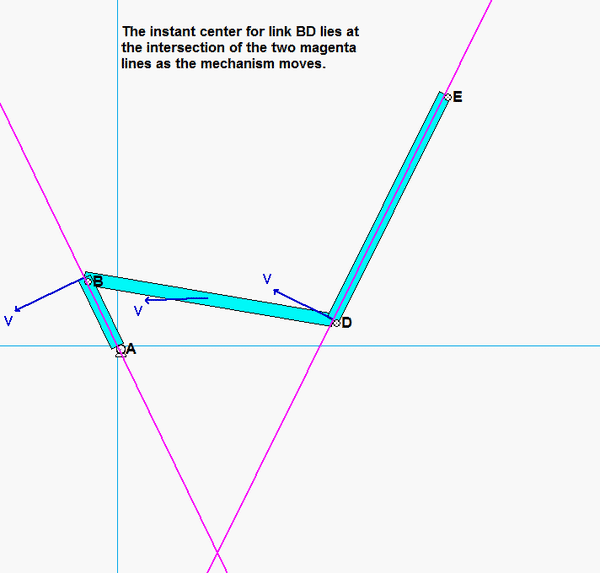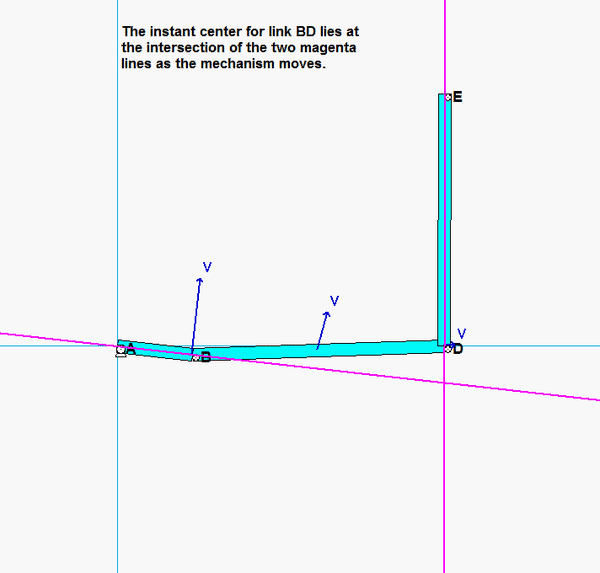
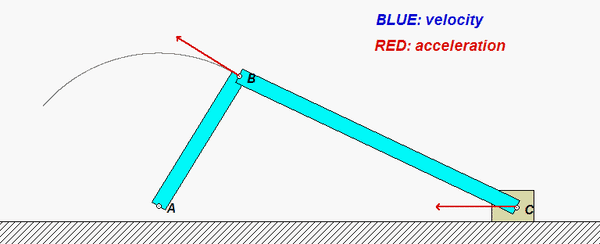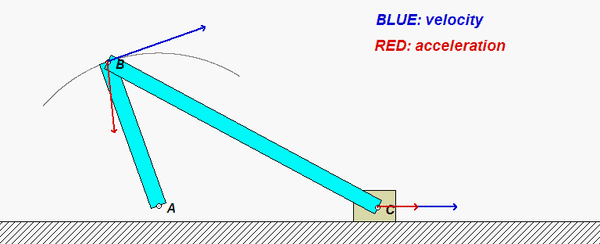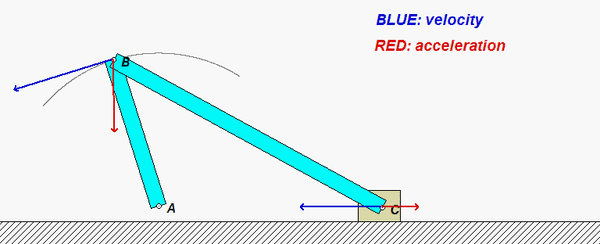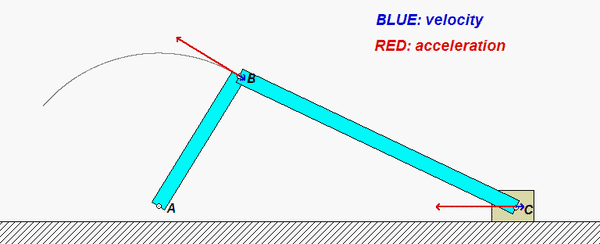
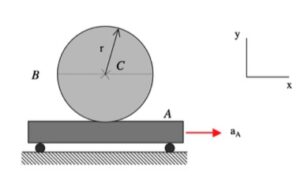
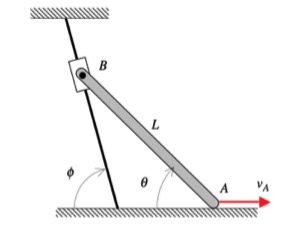
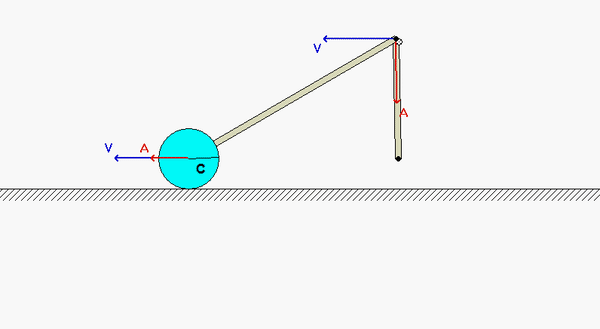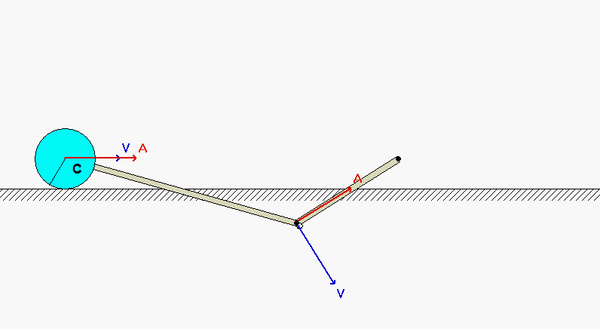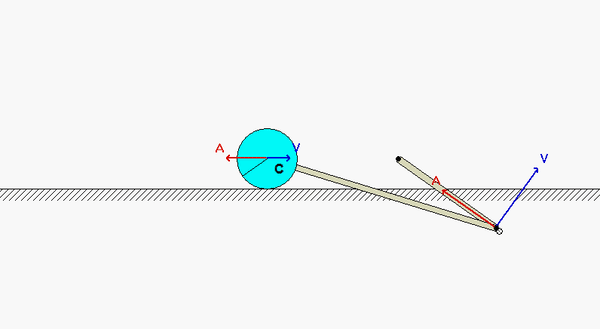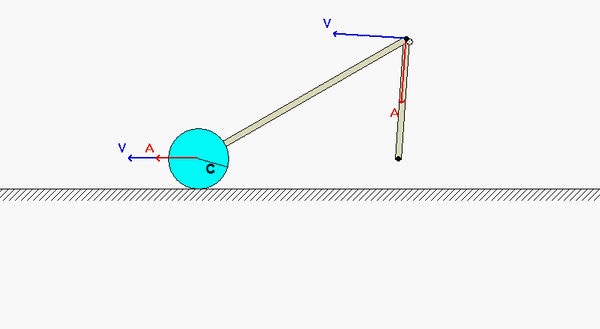
This mechanism is made up of three links: AB, BD and DE. You are given the rotation rate of link AB, and are asked to find the angular velocities and angular accelerations of links BD and DE. At the position shown, it is known that ω_AB = constant.

From the animation below, we are reminded that B and D move on circular arc paths with centers at A and E, respectively. The velocities of B and D are always perpendicular to the lines connecting the points back to the centers of the paths. Can you visualize the location of the instant center (IC) of link BD as you watch this animation? For the position of interest in this problem, you see in the animation that the velocities for all points on BD are the same – is this consistent with the location of the IC for BD at that position?

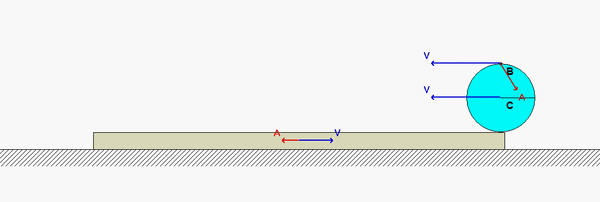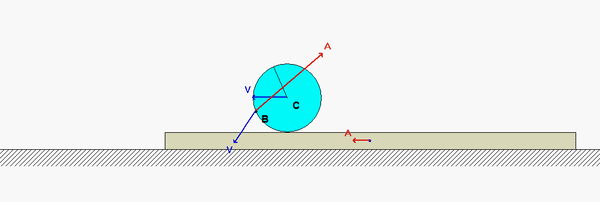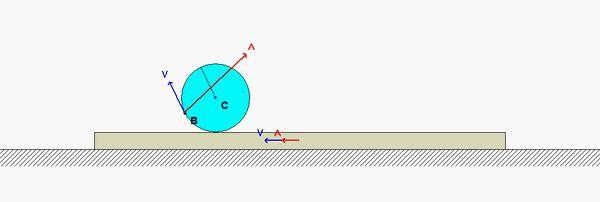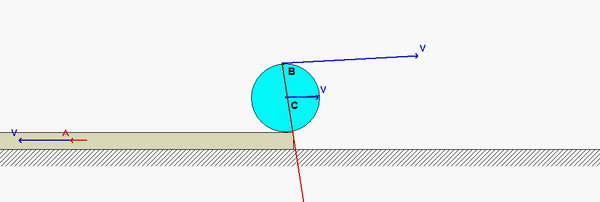
Velocity analysis
Where is the instant center of link BD? What does this location say about the angular velocity of BD?

Acceleration analysis
Write a rigid body acceleration equation for each of the three links in the mechanism:

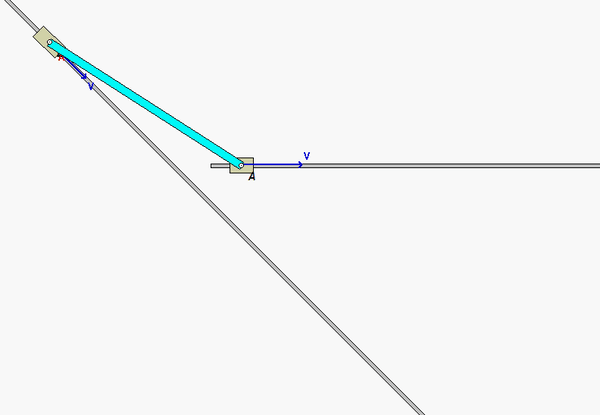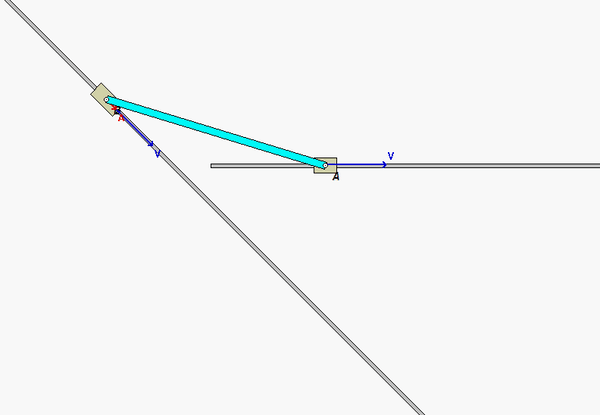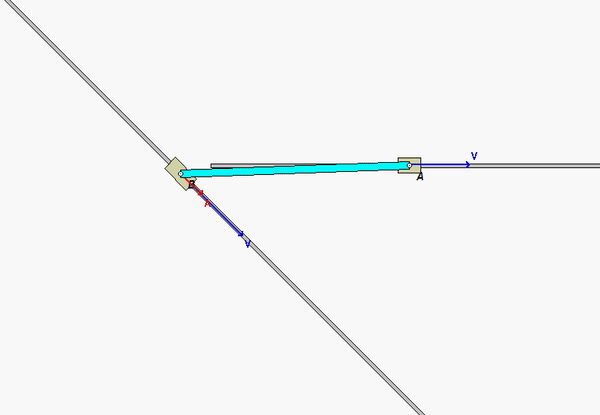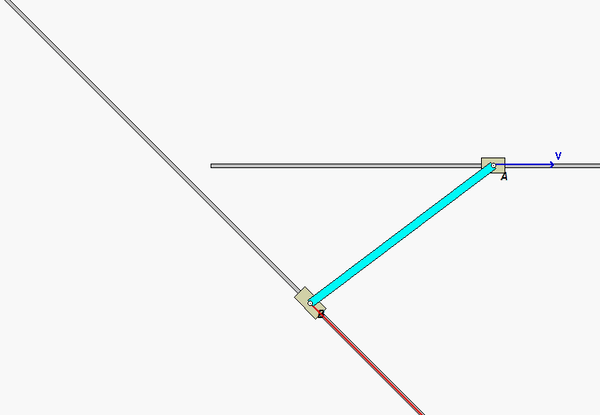
a_B = a_A + α_AB x r_B/A – ω_AB²r_B/A
a_D = a_E + α_DE x r_D/E – ω_DE²r_D/E
a_B = a_D + α_BD x r_B/D – ω_BD²r_B/D

Combining together these three vector equations in a single vector equation will produce two scalar equations in terms of α_BD and α_DE.

Shown below is a freeze-frame of the motion of the mechanism at a time corresponding to the instant on which this question is based. As can be seen the velocity for all three points on link BD are the same (in both magnitude and direction) This is consistent with the conclusion that you would make based on knowing that the IC for link BD is at infinity for this instant where AB and DE are parallel.