Discussion and hints:

Recall that for oblique impact problems, it is recommended that you use three FBDs: A alone, B alone and A+B together. A+B together allows us to make the impact force internal (and not appear in the linear impulse-momentum equation). FBDs for A and B individually allows us to determine the t-direction components of velocity each for A and B.

Step 1: FBDs
Draw FBDs of A, B and A+B.
Step 2: Kinetics (linear impulse/momentum)
Consider using the linear impulse-momentum equation for the t-direction for A and B individually, and in the n-direction for A+B. You need four equations to determine the two components of velocity for each of the two particles. Consider the coefficient of restitution as your fourth equation.
Step 3: Kinematics
Step 4: Solve
Solve for the two components of velocity for each of the two particles. From these, the post-impact direction angles of motion can be found.

Any questions?

Discussion and hints:

For this problem, make your system big. In your FBD include A, B, P and link AOB. With this choice, you can simplify your angular impulse-momentum analysis since you do not need to deal with the impact force between P and A since it will be internal to this system.

Step 1: FBDs
Draw an FBD of A, B, P and AOB together.
Step 2: Kinetics (angular impulse/momentum)
Consider the external forces acting on your system in your FBD. Which, if any, forces cause a moment about the fixed point O? Write down the angular momentum for each particle individually and add together to find the angular momentum for your system: H_O = 2m r_A/O x v_A + m r_B/O x v_B + m r_C/O x v_C. Is this momentum conserved? Also, consider using the coefficient of restitution equation.
Step 3: Kinematics
Use the rigid body velocity equation to relate the velocities of A and B.
Step 4: Solve
Use your results from Steps 3 and 4 to solve for the angular speed of AOB.

Any questions?

Ask and answer questions here. You learn both ways.

DISCUSSION and HINTS

Recall the definition of angular momentum of a particle P (of mass m) about a fixed point O:  H_O = m r_P/O x v_P.

For this problem, use this equation to find the angular momentum of the particle about the three fixed points A, B and C. Are any of these three values zero? If so, why does it equal zero?

Ask and answer questions here. You learn both ways.

DISCUSSION and HINTS

Recall the following four-step plan outline in the lecture book and discussed in lecture:

Step 1: FBDs
Draw a free body diagram (FBD) of P.

Step 2: Kinetics (Work/energy and linear impulse/momentum)
Since the only force acting on P acts through the fixed point O, there are no moments about O acting on P. Therefore, angular momentum about O is conserved. Note that this equation produces a value for the angular speed ω of the cord, but it does not provide us information on R_dot. Why is that?

Now consider the work/energy equation. There is no change in potential energy. The work done by F is simply F*ΔR. This equation will allow you to solve for the speed of P at the second state.

Step 3: Kinematics
Use the magnitude of the velocity vector to provide the equation that you need to solve for R_dot: v² = R_dot² + (Rω)².

Step 4: Solve
Solve for R_dot, and then write out the vector answer for the velocity of P at the second state.

Ask and answer questions here. You learn both ways.

DISCUSSION and HINTS

You need to break the problem into two parts: during impact and between post-impact and the maximum rotation angle of the bar. For the during impact portion, consider the following:

Step 1: FBDs
Draw a single free body diagram including the two pendulum masses, the bullet and the bar.

Step 2: Kinetics (linear impulse/momentum)
Is angular momentum for the system about point O conserved? If so, why? Energy is NOT conserved. Why?

Step 3: Kinematics
After impact, the velocity of the bullet is the same as the velocity of the lower pendulum mass. You need to relate the speeds of the two pendulum masses and the bullet to the angular speed of the bar using rigid body kinematics.

Step 4: Solve
From your equations solve for the velocities of the two pendulum masses and the bullet.

After impact, consider using conservation of energy for the system of the two pendulum masses and the bullet together.

Ask and answer questions here. You learn both ways.

DISCUSSION and HINTS

Recall the definition of angular momentum of a particle P (of mass m) about a fixed point O:  H_O = m r_P/O x v_P.

For this problem, use this equation to find the angular momentum for each particle and add these together. As you work the problem, consider the number of cancellations that occur among these terms and consider why these cancellations occur. This will help you get insights on the meanings of angular momentum.

Ask and answer questions here. You learn both ways.

DISCUSSION and HINTS

Recall the following four-step plan outline in the lecture book and discussed in lecture:

Step 1: FBDs
Draw a free body diagram of the ball during impact with the bumper cushion. Identify the n- and t-directions on your FBD.

Step 2: Kinetics (linear impulse/momentum)
Are there forces acting on the ball in the t-direction? If not, linear momentum is conserved in that direction

Are there forces acting on the ball in the n-direction? There is a force, so don't even think about conservation of linear momentum in that direction.

Use the coefficient of restitution to relate the n-components of velocity of the ball before and after impact.

Step 3: Kinematics
Calculate the rebound angle needed for the ball after impact for the ball to be dropped into the corner pocket.

Step 4: Solve
From your equations solve for the angle of incidence for the ball.

Ask and answer questions here. You learn both ways.

DISCUSSION and HINTS

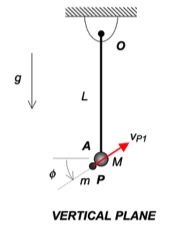
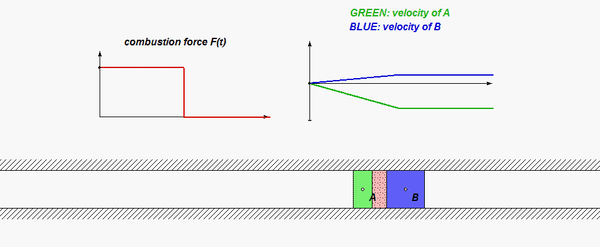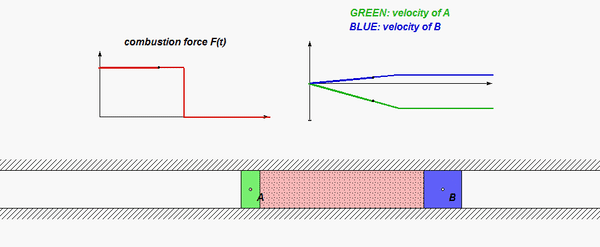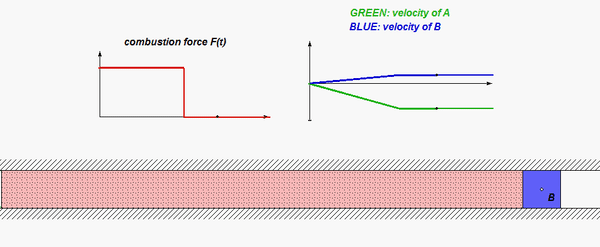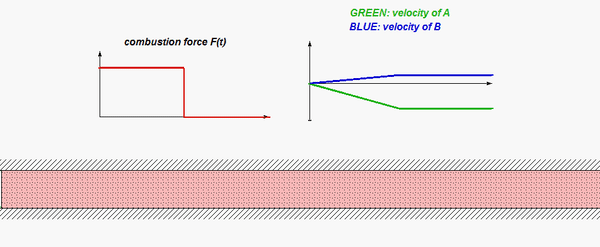
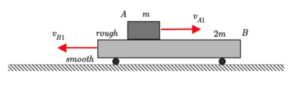
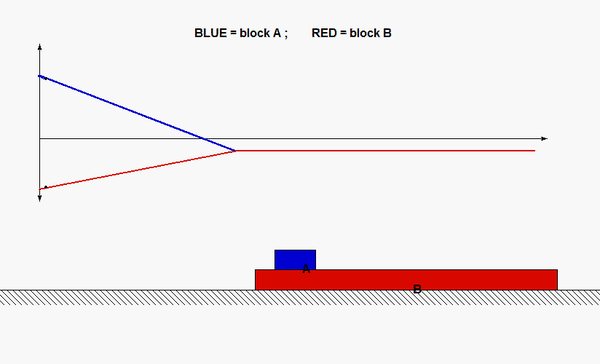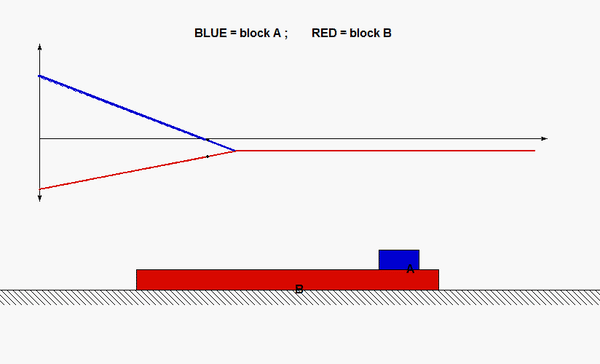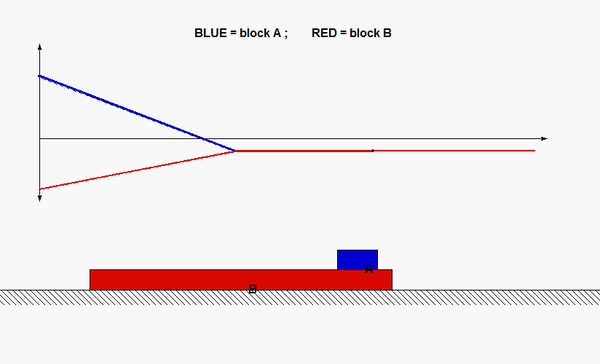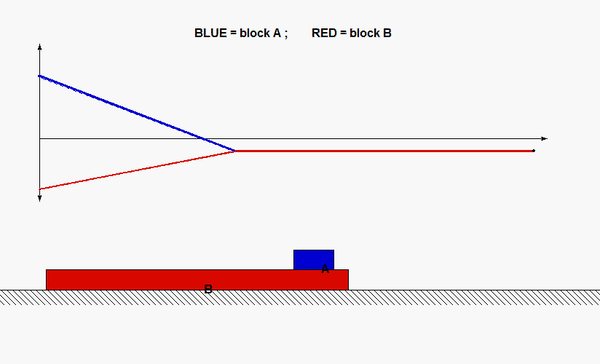
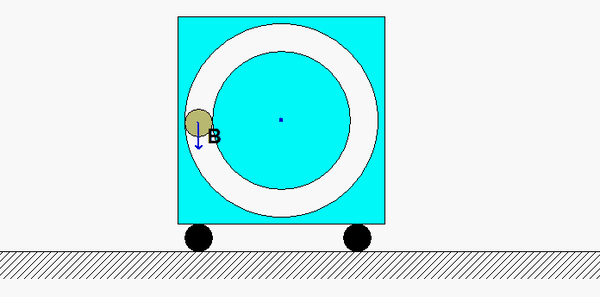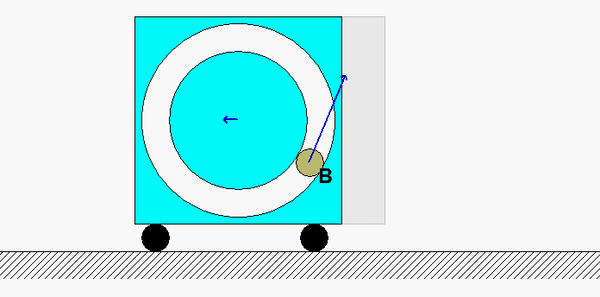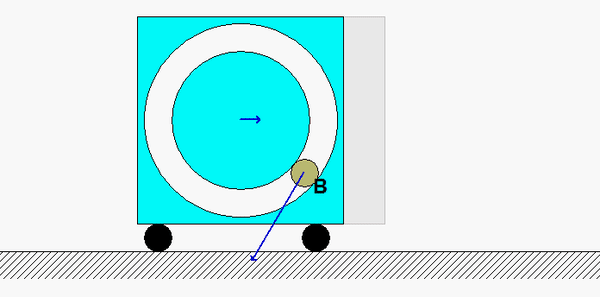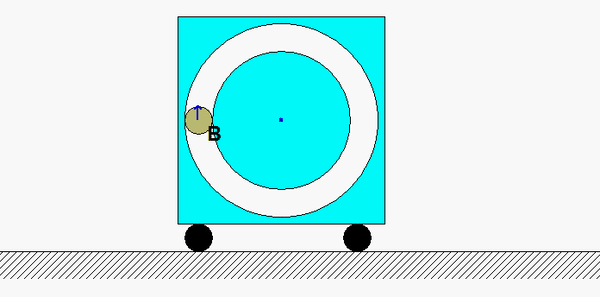
This is a standard problem for the central impact of two bodies.

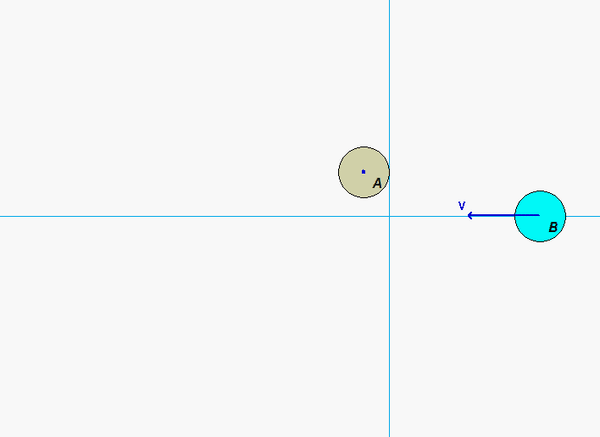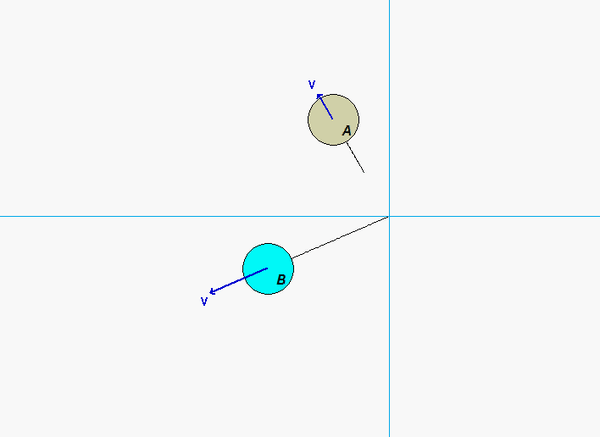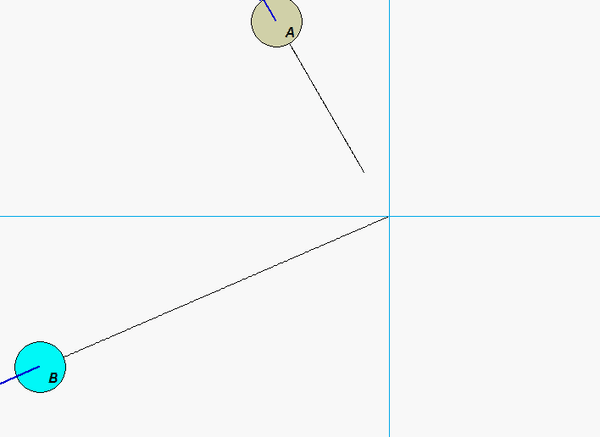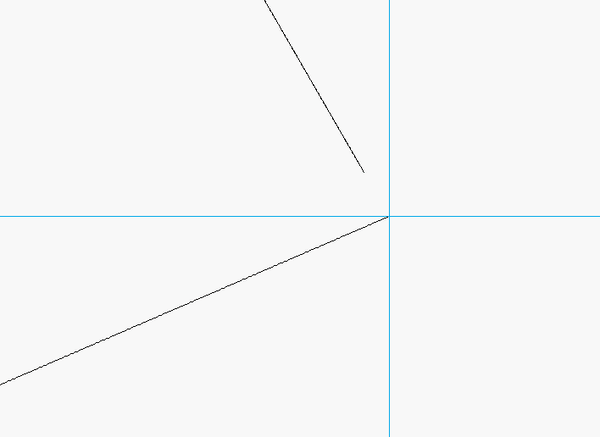
Recall the following four-step plan outline in the lecture book and discussed in lecture:

Step 1: FBDs
Draw three free body diagrams (FBDs): one of A alonw, one of B alone and one of A+B. Identify the n- and t-directions on your FBDs.

Step 2: Kinetics (linear impulse/momentum)

• In which directions, if any, is linear momentum conserved for A alone? For those direction(s), write down the appropriate momentum conservation equation.
• In which directions, if any, is linear momentum conserved for B alone? For those direction(s), write down the appropriate momentum conservation equation.
• In which directions, if any, is linear momentum conserved for A+B? For those direction(s), write down the appropriate momentum conservation equation.
• Recall that you also have the coefficient of restitution (COR) equation at your disposal. Keep in mind that the COR equation is valid for only the n-components of velocity.

Step 3: Kinematics
None needed here.

Step 4: Solve
From your equations solve for the n- and t-components of velocity of A and B.

Ask and answer questions here. You learn both ways.

DISCUSSION and HINTS

Shown below is a simulation of an experiment of dropping a ball onto a fixed surface. Before impact and after impact, energy is conserved. During impact, a large impact force is generated. Although we cannot calculate the details of the force during impact, we can use the impulse/momentum equation to calculate the average force during impact. Note that this experiment differs from your problem in terms of the duration of the impact, with your impact duration being only 20% of the duration shown here.

Parts (a)-(c)
Draw two FBDs for the duration of time that includes only the impact: one FBD with weight, and one without weight. Sum forces on the particle in the vertical direction. Use the linear impulse/momentum equation relating the change in linear momentum during the impact to the impulse of the forces acting on the particle during impact. Compare your with and without gravity answers.

Part (d)
Although energy is not conserved during impact, energy is conserved prior to and after impact. Use conservation of energy before and after impact to relate h₁ and h₂.

Ask and answer questions here. You learn both ways.

DISCUSSION and HINTS

Recall the following four-step plan outline in the lecture book and discussed in lecture:

Step 1: FBDs
Draw single free body diagram (FBD) for the entire system (B + slotted block). Do NOT consider A and B in separate FBDs!

Step 2: Kinetics (Work/energy and linear impulse/momentum)
Consider all of the external forces that you included in your FBD above.

• Which forces, if any, do non-conservative work on that system? If there are no such forces, then energy is conserved. Write down the expressions for kinetic and potential energy (of B+block) for the initial and final states of the motion.
• Now, which external forces have components in the horizontal direction (x-direction_? If none, then linear momentum (of B+block) in that direction is conserved.

Step 3: Kinematics
At position 1 the system is at rest. At Position 2, both the block and B have only x-components of velocity; that is, v_B = v_Bx.

Step 4: Solve
Combine your kinetics equation from Step 2 with your kinematics that you found in Step 3, and solve for the velocities of A and B.