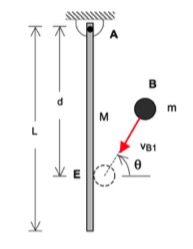
| Problem statement Solution video |
DISCUSSION THREAD

Discussion and hints:
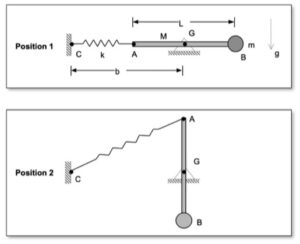
Recall the following four-step plan outline in the lecture book and discussed in lecture:
Step 1: FBDs
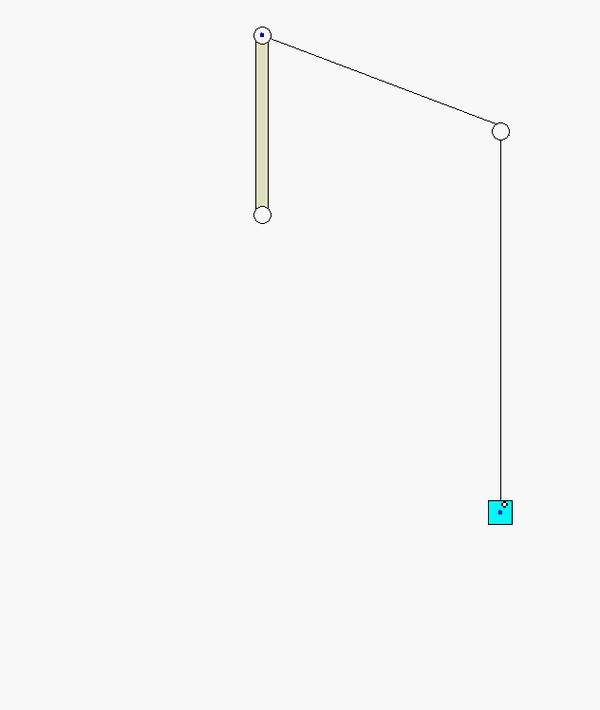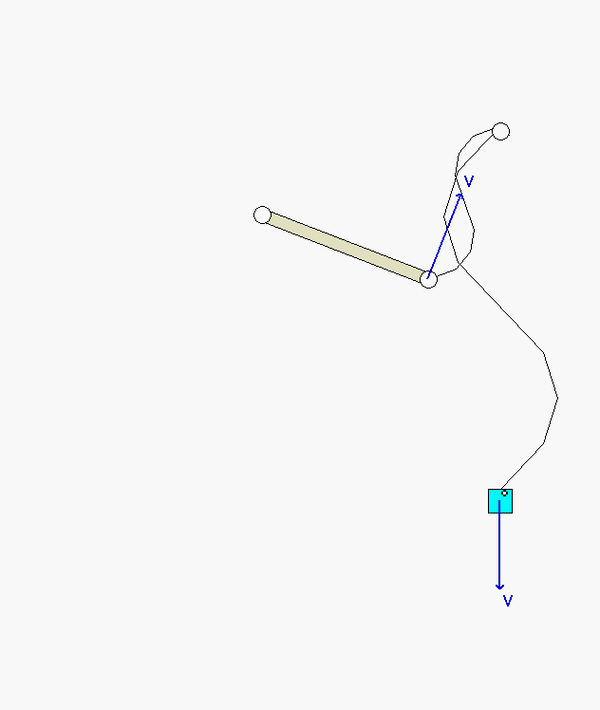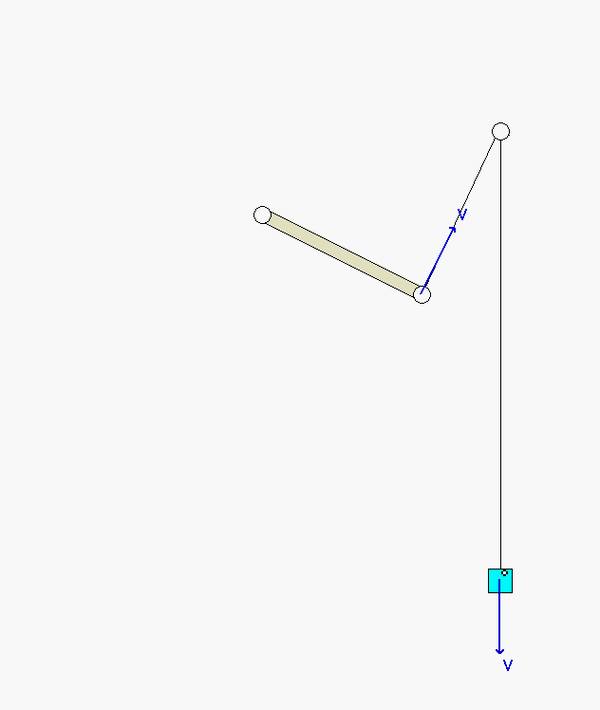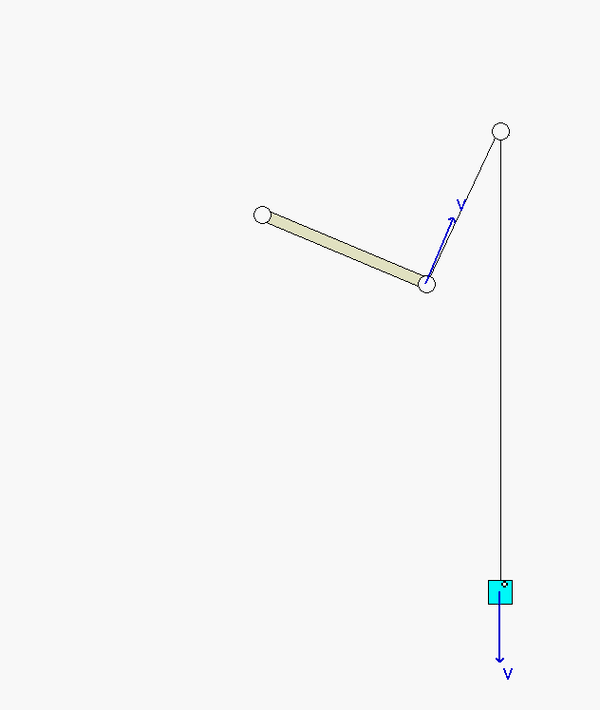
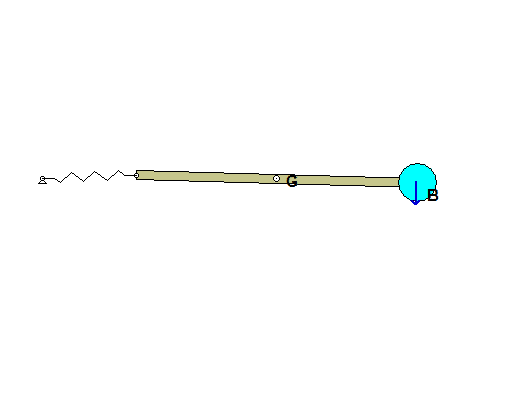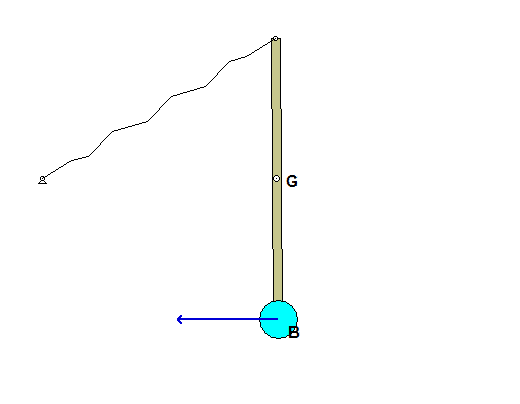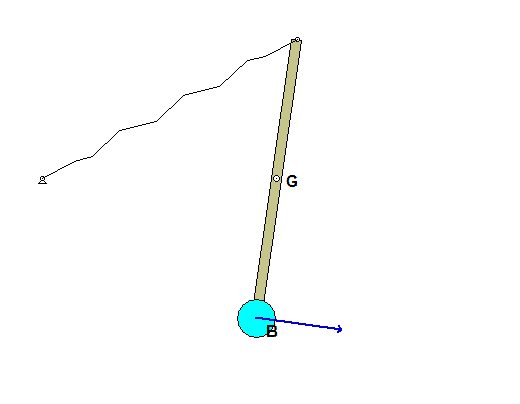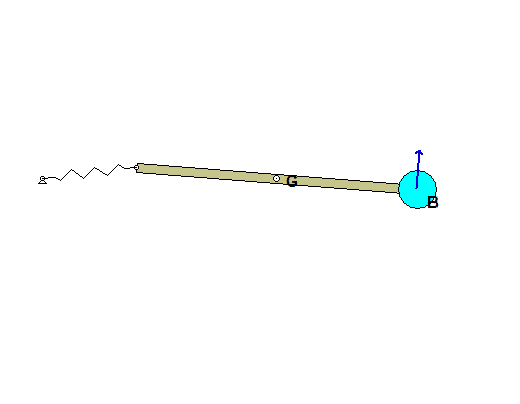
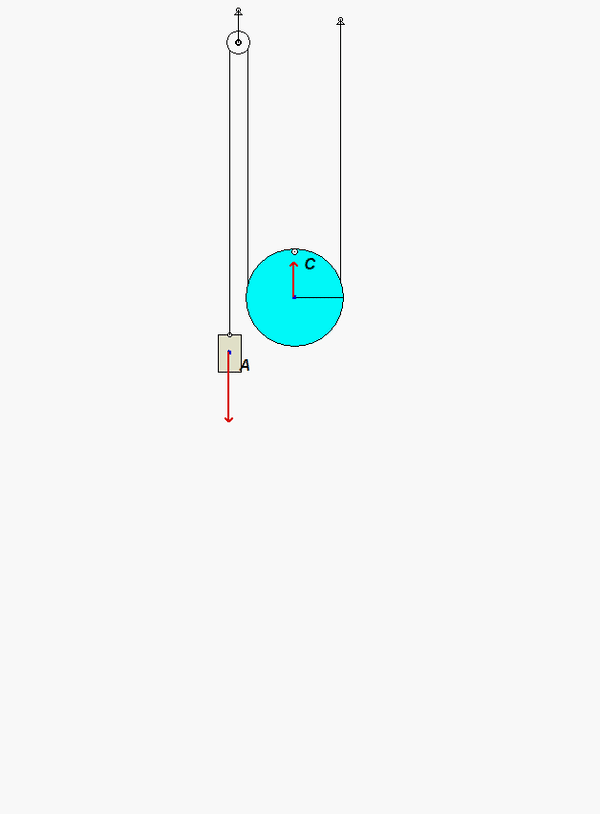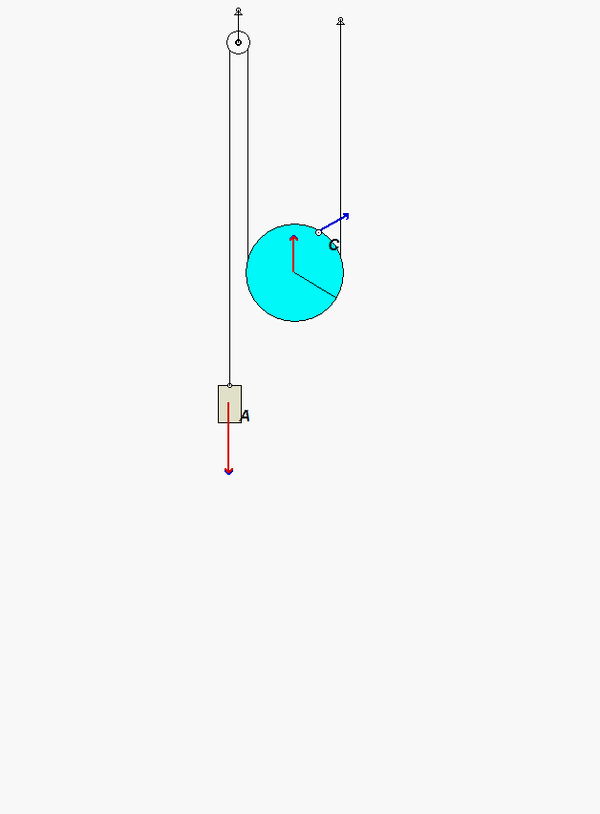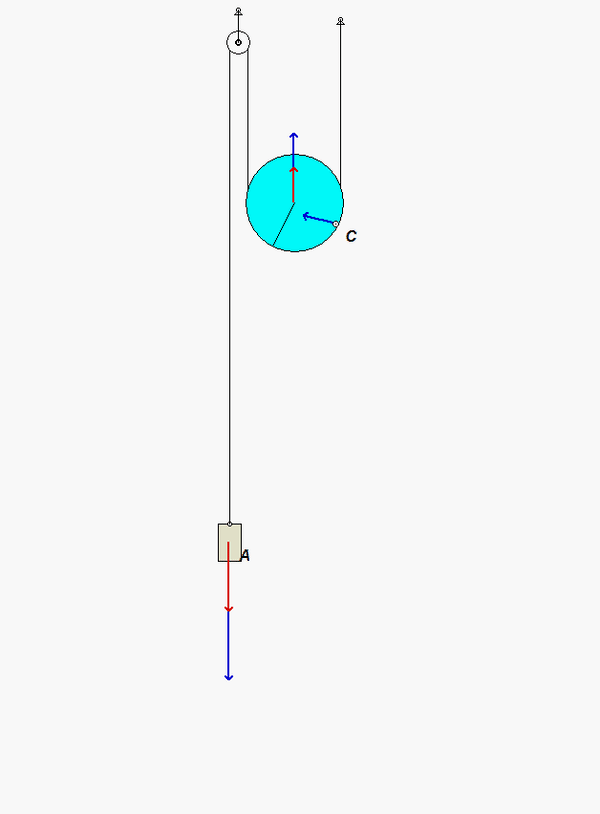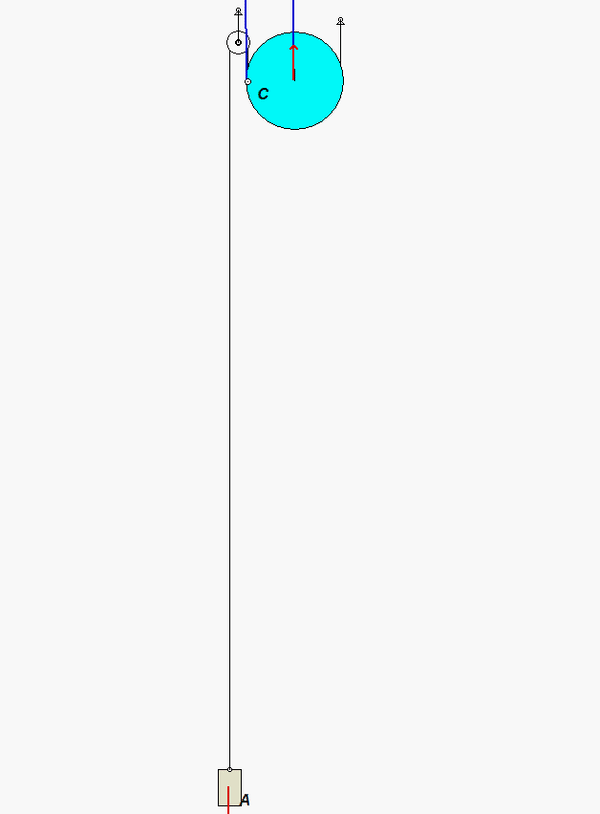
Draw individual free body diagrams for block A and the disk on the right. It is recommended that in drawing the FBD of the disk, include both the disk and the section of wrapped cable in the FBD, as shown below. This allows to you make the interaction forces between the cable and the disk "internal", greatly simplifying the FBDs. Also, please note that the cable tensions TB and TC are NOT the same.
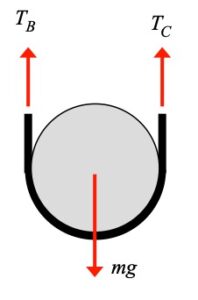
Step 2: Kinetics (Newton/Euler)
Write down the Newton/Euler equations for the block and the disk using your FBDs above. Take care in choosing the reference point for your moment equation for the disk. In order to use the "short form" of Euler's equation, this point should be either a fixed point, the body's center of mass, or a point whose acceleration is parallel to the vector connecting that point to the center of mass of the body. For this problem, there are no fixed points. However, the latter two options will apply. You might consider using point C since its acceleration will always point toward the center of mass of the disk. If you are not confident with this, then stick with the center of mass of the disk.
Step 3: Kinematics
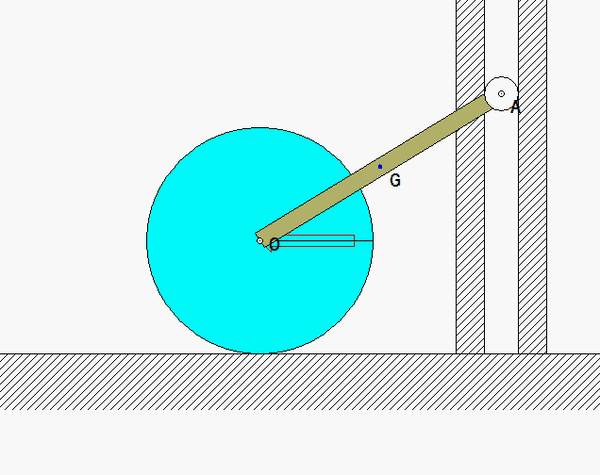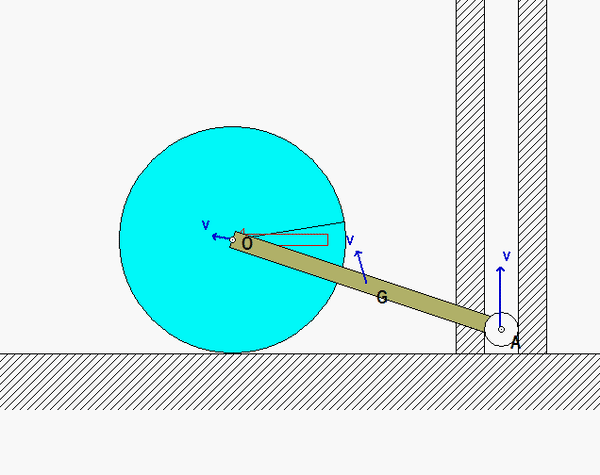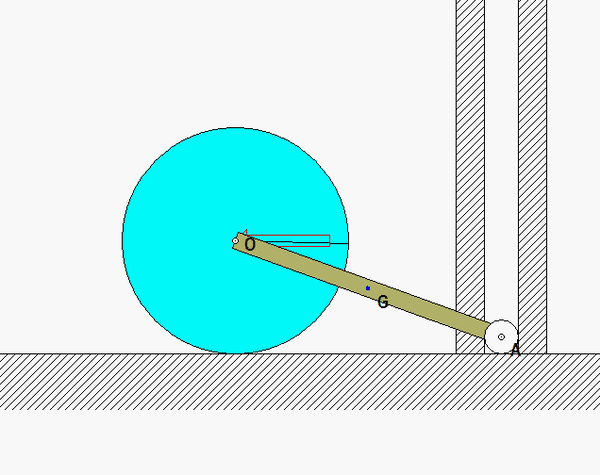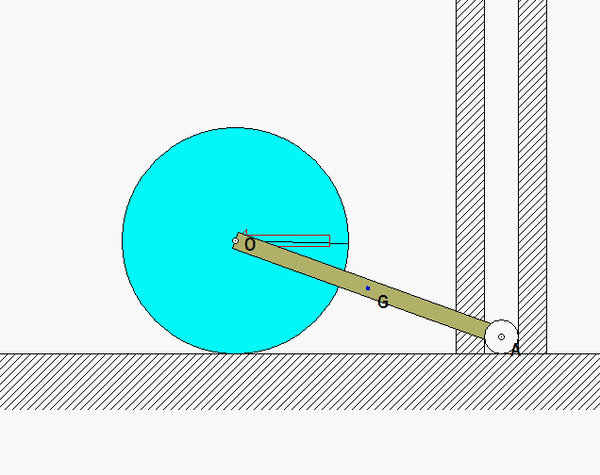
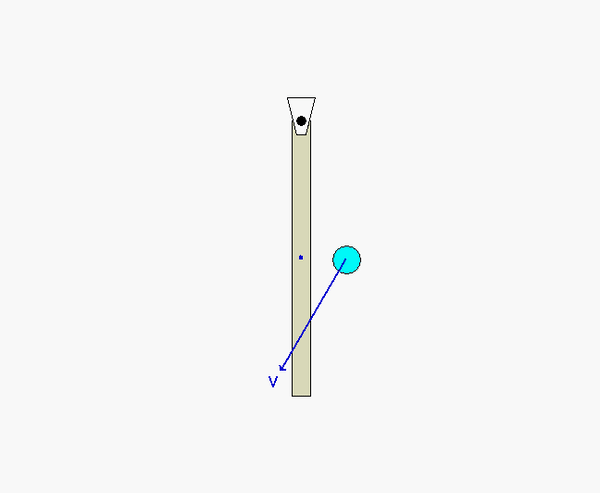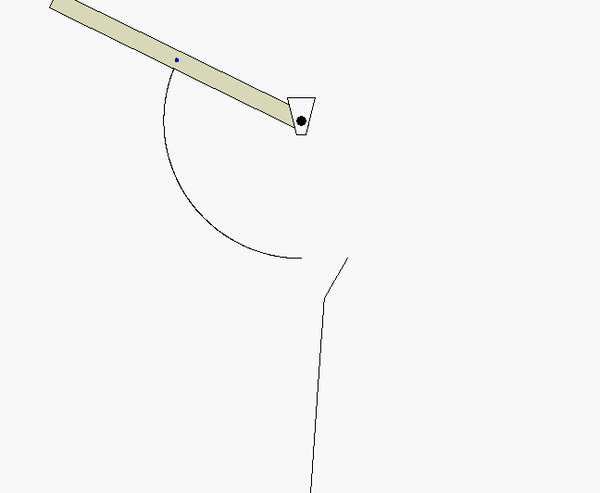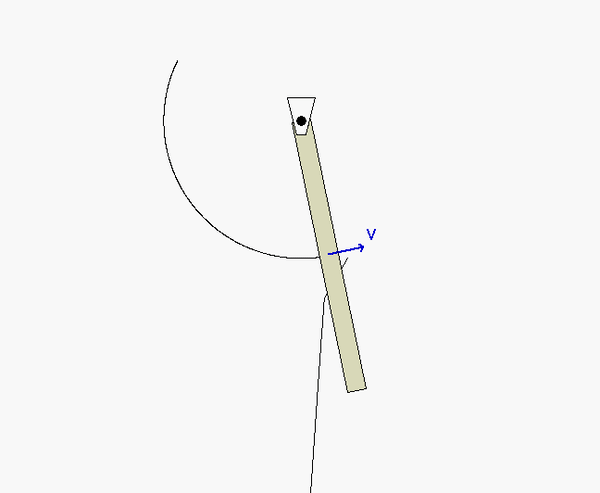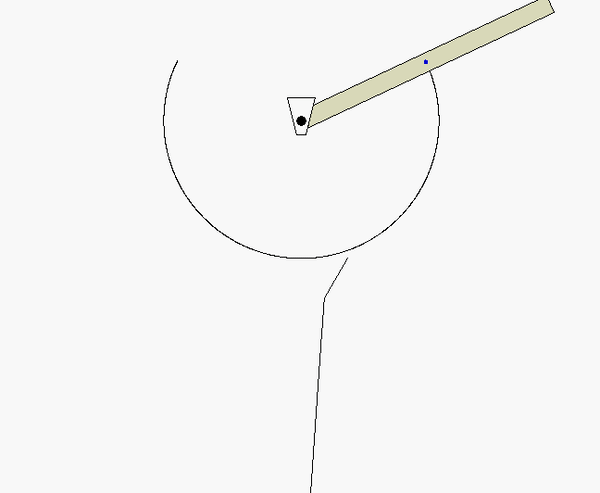
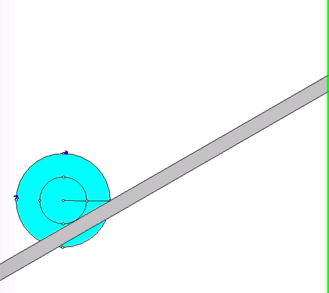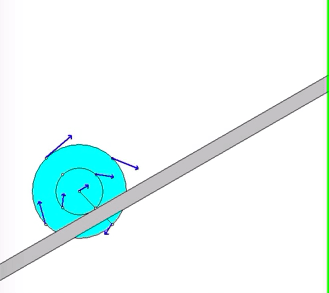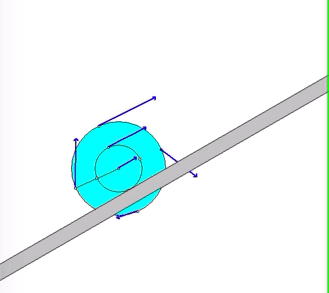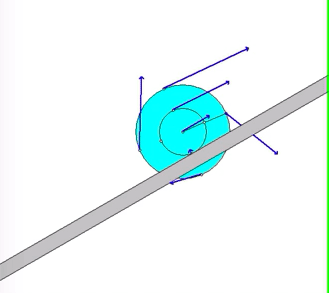
Put some thought into the kinematics for this problem. Note that the contact point on the disk with the cable on the right side (point C) is the instant center for the disk. (Recall that the cable does not slip on the disk. Since the cable on the right side is stationary, then so is point C on the disk.) This is apparent when you view the animation above of the system as it moves - as point C moves into contact with the cable, its velocity is zero. This will assist you in being able to relate the motions of the center of the disk to the motion of block A.
Recall that since C is the IC of the disk, it can have, at most, a component of acceleration in the x-direction. With this, you can use the kinematic analysis below to relate the acceleration of the center of mass of the disk to its angular acceleration, and to relate the accelerations of the disk center of mass of point B.
 NOTE: The acceleration of A is NOT equal to the acceleration of the center of the disk. Ask questions here on the blog if this is not clear.
NOTE: The acceleration of A is NOT equal to the acceleration of the center of the disk. Ask questions here on the blog if this is not clear.
Step 4: Solve
Solve your equations above for the acceleration of block A.
Any questions?