Ask your questions here. Or, answer questions of others here. Either way, you can learn.

DISCUSSION and HINTS

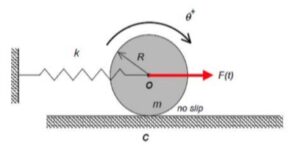
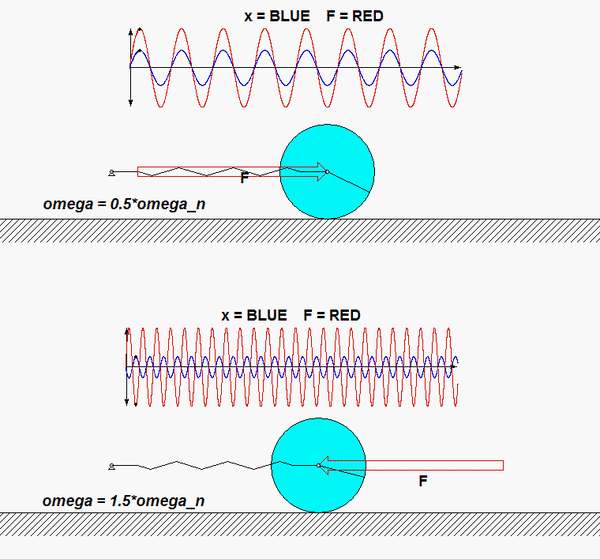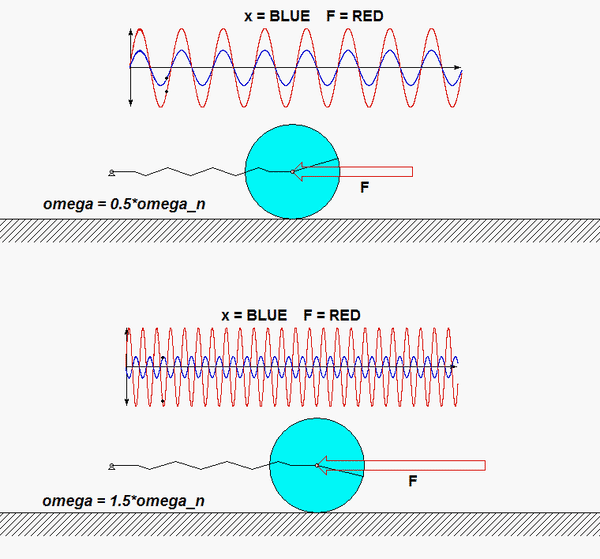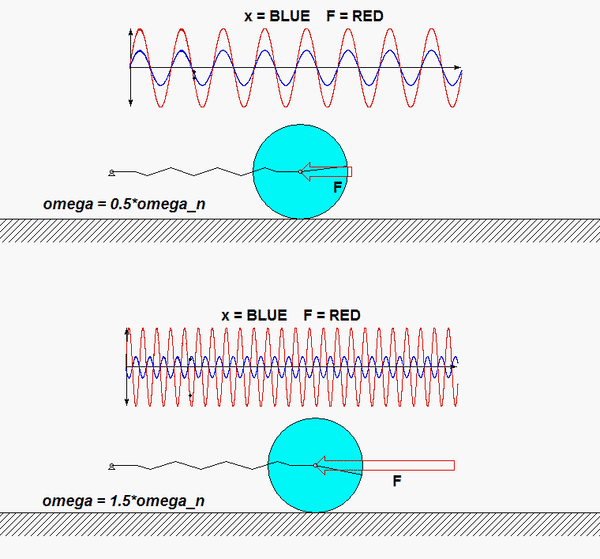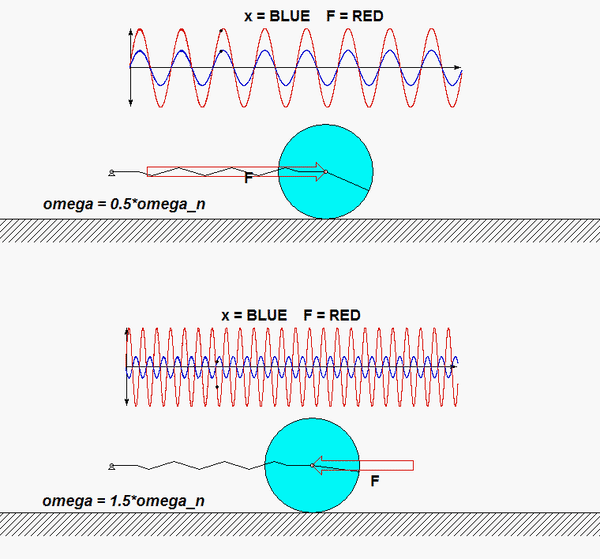
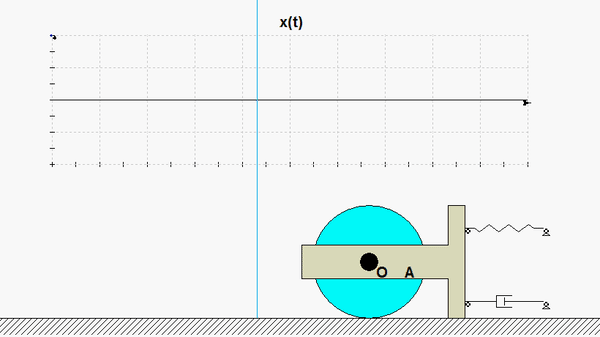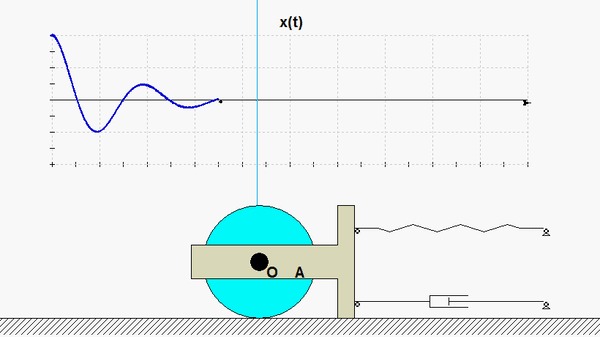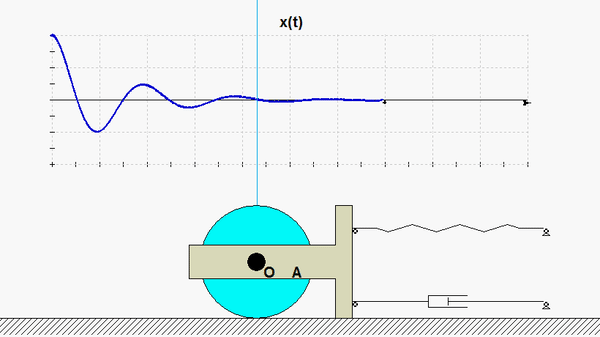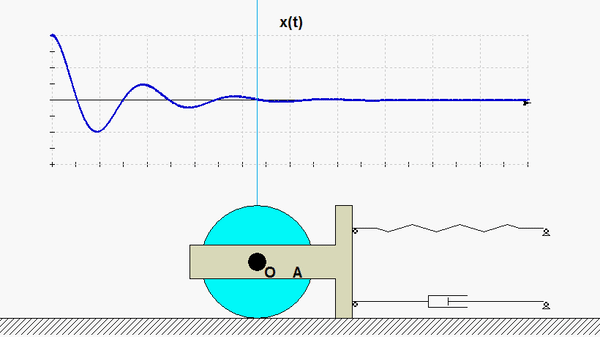
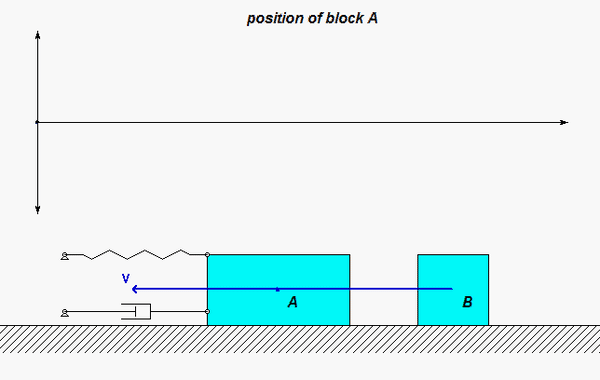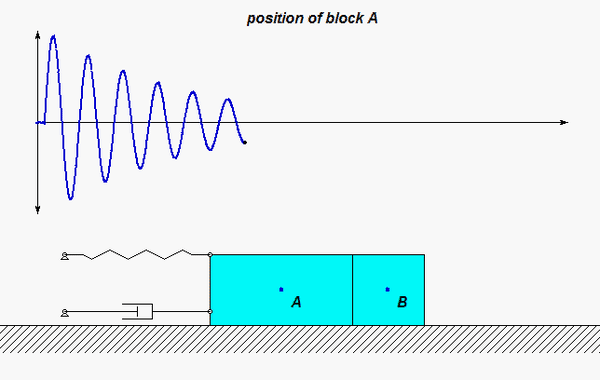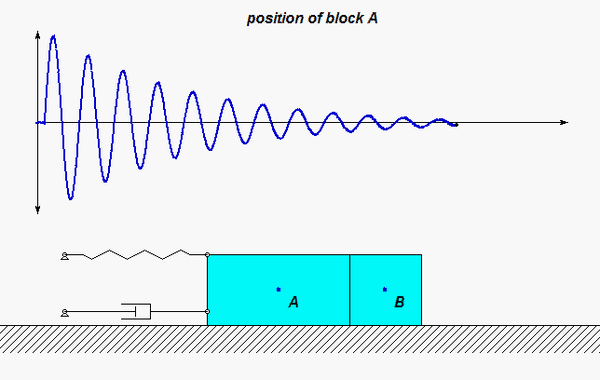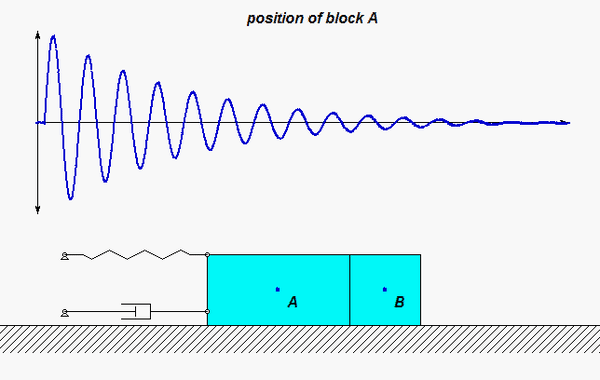
In this problem, the excitation does not come from a prescribed force, but, instead, it arises from a prescribed displacement on one body in the system. The support B here is given a prescribed motion of x_B(t) = b sinωt, where ω is the frequency of excitation. Our goal is to solve for the particular solution of the response. Shown below is an animation of this forced response for a given value of excitation frequency? Can you tell from watching the motion of the system if the excitation frequency is less than or greater than the natural frequency of the system?

Recall the following four-step plan outline in the lecture book and discussed in lecture:

Step 1: FBDs
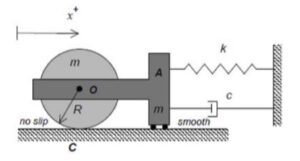
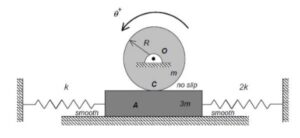
Draw a free body diagram (FBD) of the disk. You will need to temporarily define a coordinate representing the rotation of the disk. For example, you could use the angle θ as the angle of rotation for the disk, measured positive in the clockwise direction. Take care in getting the directions correct on the spring forces acting on the disk. Also, be sure to include the friction force acting on the disk by the cart B. Note that you do NOT need an FBD of B since you already know its motion.

Step 2: Kinetics (Newton/Euler)
Write down both Newton’s 2nd law and Euler’s equation for the disk. Note that with C being the no-slip point on the disk: ΣM_C ≠ I_C α.  Why is that?

Step 3: Kinematics
Here you need to relate x_ddot to θ_ddot. How do you do this? Please note that C is an accelerating point on the disk.

Step 4: EOM
Combine your results from Step 2 and Step 3 to arrive at your EOM.

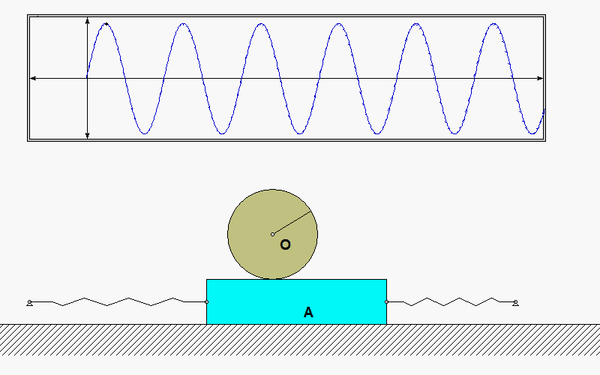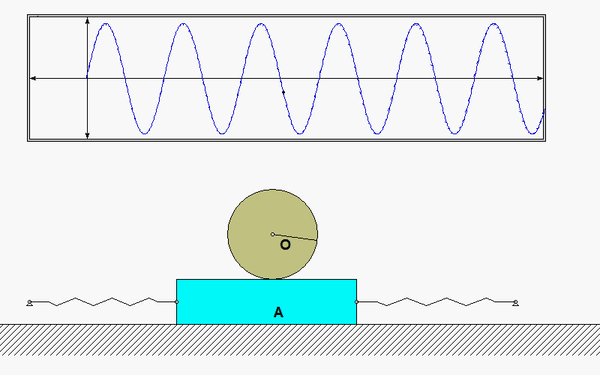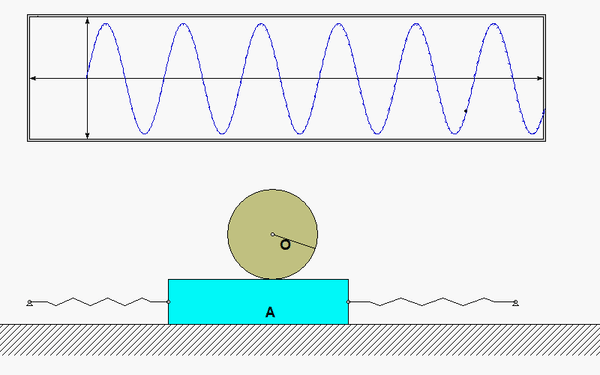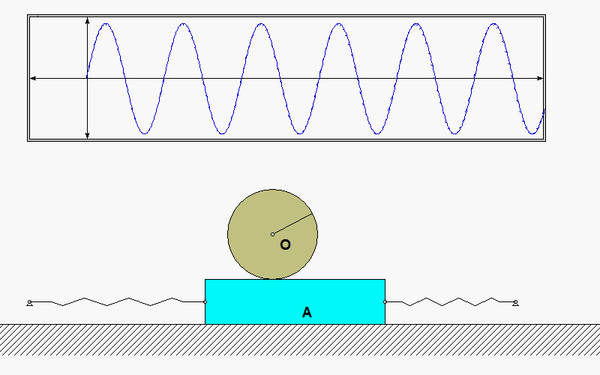
Once you have determined the EOM for the system, identify the natural frequency from the EOM. From the EOM we know that the particular solution of the EOM is given by: x_P(t) = A*sin(ωt)+ B*sin(ωt). How do you find the forced response coefficients A and B? And, how do you determine the phase of this forced response?

Any questions?

Ask your questions here. Or, answer questions of others here. Either way, you can learn.

DISCUSSION and HINTS

Recall the following four-step plan outline in the lecture book and discussed in lecture:

Step 1: FBDs
Draw a free body diagram (FBD) of block A.

Step 2: Kinetics (Newton/Euler)
Use Newton’s 2nd law to write down the dynamical equation for the system in terms of the coordinate x. Be careful with the directions of your spring forces, and that these are consistent with the coordinate x defined. here.

Step 3: Kinematics
None needed here.

Step 4: EOM
Your EOM was found at Step 2.

Once you have determined the EOM for the system, identify the natural frequency from the EOM. From the EOM we know that the particular solution of the EOM is given by: x_P(t) = A*sin(ωt)+ B*cos(ωt). How do you find the forced response coefficients A and B?

Ask your questions here. Or, answer questions of others here. Either way, you can learn.

DISCUSSION and HINTS

The particular solution for the equation of motion for this system is shown below for two values of the frequency of excitation, ω. As we have seen in lecture, and as shown below, when the excitation frequency is less than the natural frequency,ω_n, the response is in phase with the excitation, and when the frequency is greater than ω_n, the response is 180° out of phase with the excitation. Can you see this in the animations below?

Recall the following four-step plan outline in the lecture book and discussed in lecture:

Step 1: FBDs
Draw a free body diagram (FBD) of the disk. It is important to temporarily define a translation coordinate that describes the position of the center of the disk, O. Let’s call that variable x, and have it defined as being positive to the right.

Step 2: Kinetics (Newton/Euler)
Use Euler’s equation about the no-slip contact point C.

Step 3: Kinematics
Relate x_ddot to θ_ddot through kinematics.

Step 4: EOM
Combine your equations from Steps 2 and 3 to arrive at your EOM in terms of θ.

Once you have determined the EOM for the system, identify the natural frequency from the EOM. From the EOM we know that the particular solution of the EOM is given by: theta_P(t) = A*sin(ωt)+ B*cos(ωt). How do you find the forced response coefficients A and B?

Does your result here agree with the expected relationship between excitation frequency and response with regard to the “phase” of the solution?

Ask your questions here. Or, answer questions of others here. Either way, you can learn.

DISCUSSION and HINTS

Recall the following four-step plan outline in the lecture book and discussed in lecture:

Step 1: FBDs
Draw individual free body diagrams (FBDs) of the wheel and block A.   Don’t forget the equal-and-opposite pair of reaction forces acting between the wheel and the block atO. It is important to temporarily define a coordinate that describes the rotation of the wheel. Let’s call this θ,  and define it to be positive in the clockwise sense.

Step 2: Kinetics (Newton/Euler)
Using your FBDs from above, write down the Euler equation for the disk (about the no-slip point C), and the Newton equation for the block. Combine these two equations into a single equation through the elimination of the reaction forces at O for the equations.

Step 3: Kinematics
You need to relate the angular acceleration of the disk and the acceleration of the block. How is this done? What are the results?

Step 4: EOM
From your equations in Steps 2 and 3, derive the equation of motion (EOM) of the system in terms of x.

Once you have determined the EOM for the system, identify the natural frequency, damping ratio and the damped natural frequency from the EOM. Also, from the EOM we know that the response of the system in terms of x is given by: x(t) = e^-ζω_nt [C*cos(ω_dt)+ S*sin(ω_dt)]. How do you find the response coefficients C and S?

Ask your questions here. Or, answer questions of others here. Either way, you can learn.

DISCUSSION and HINTS

After block B strikes and sticks to block A, the two blocks move together as a single rigid body. In deriving your equation of motion here, focus on a system with a single block (of mass 3m) connected to ground with a spring and dashpot.

Recall the following four-step plan outline in the lecture book and discussed in lecture:

Step 1: FBDs
Draw a free body diagram (FBD) of A+B.

Step 2: Kinetics (Newton/Euler)
Use Newton’s 2nd law to write down the dynamical equation for the system in terms of the coordinate x.

Step 3: Kinematics
None needed here.

Step 4: EOM
Your EOM was found at Step 2.

Once you have determined the EOM for the system, identify the natural frequency, damping ratio and the damped natural frequency from the EOM. Also, from the EOM we know that the response of the system in terms of x is given by: x(t) = e^-ζωnt [C*cos(ω_dt)+ S*sin(ω_dt)]. How do you find the response coefficients C and S? What will you use for the initial conditions of the problem? (Consider linear momentum of A+B during impact.)

Ask your questions here. Or, answer questions of others here. Either way, you can learn.

DISCUSSION and HINTS
As the system moves, there is no slipping between the contact point C on the drum and block A.  This represents a constraint between the drum rotation and the block translation. We will deal with this in Step 3 of the derivation of the equation of motion below.

Recall the following four-step plan outline in the lecture book and discussed in lecture:

Step 1: FBDs
Draw individual free body diagrams (FBDs) of the drum and the disk. Be sure to include the equal-and-opposite contact forces on both the drum and the block. It is important to temporarily define a coordinate that describes the motion of the block. Let’s call that variable “x“, and define it to be positive to the right. With this definition, the spring forces on the left and right side of the block are kx and 2kx, respectively, with both forces pointing to the left.

Step 2: Kinetics (Newton/Euler)
Using your FBDs from above, write down the Euler equation for the drum, and the Newton equation for the block. Combine these two equations through the elimination of the drum-to-block contact force.

Step 3: Kinematics
You need to relate the angular acceleration of the drum to the acceleration of the block. How is this done? What are the results? Also, how do you relate the stretch/compression x in the two springs in terms of θ?

Step 4: EOM
From your equations in Steps 2 and 3, derive the equation of motion (EOM) of the system in terms of θ.

Once you have determined the EOM for the system, identify the natural frequency from the EOM. Also from the EOM, we know that the general form of the response is: θ(t) = C*cos(ω_nt)+ S*sin(ω_nt). How do you find the response coefficients C and S?

Ask your questions here. Or, answer questions of others here. Either way, you can learn.

DISCUSSION and HINTS

Recall the following four-step plan outline in the lecture book and discussed in lecture:

Step 1: FBDs
Draw individual free body diagrams (FBDs) of the two disks and block A.  Note that the tension forces in the different sections of the cable are NOT equal. It is important to temporarily define coordinates that describe the rotations of the two disks. Let’s call these θ_C and θ_O,  and define these to be positive in the clockwise sense.

Step 2: Kinetics (Newton/Euler)
Using your FBDs from above, write down the Euler equations for the two disks, and the Newton equation for the block. Combine these three equations into a single equation through the elimination of the tension forces for the equations.

Step 3: Kinematics
You need to relate the angular acceleration of the disks and the acceleration of the block. How is this done? What are the results?

Step 4: EOM
From your equations in Steps 2 and 3, derive the equation of motion (EOM) of the system in terms of x.

Once you have determined the EOM for the system, identify the natural frequency from the EOM. Note that the static deformation of the system is found by setting x_ddot = 0 in the EOM.