Discussion and hints:

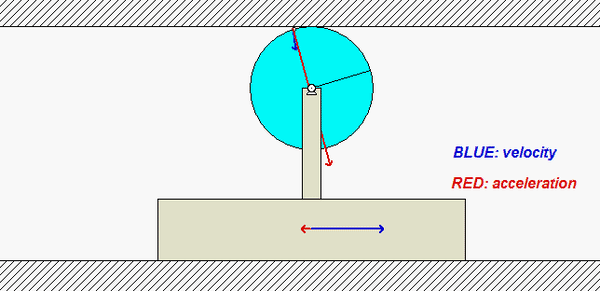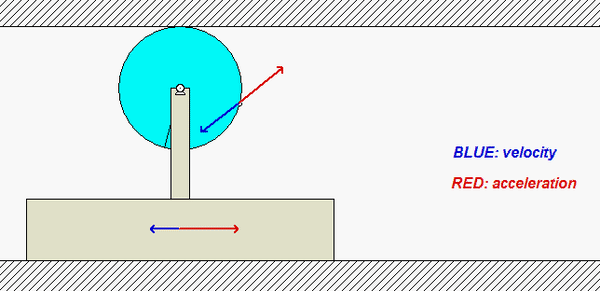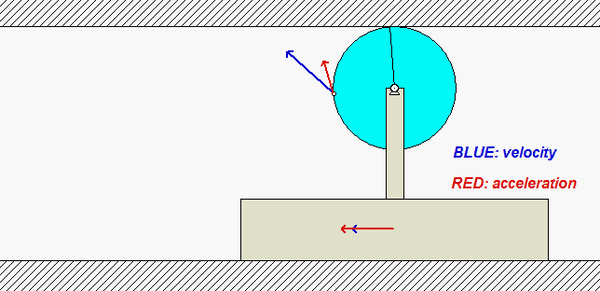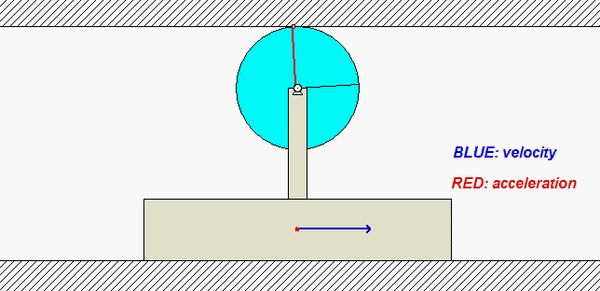
Note that since the top contact point of the disk rolls without slipping on the upper fixed surface, this contact point has zero velocity. In addition, the horizontal component of acceleration of that point is also zero (the vertical component of acceleration is NOT zero, however).

For the velocity problem, write down the velocity kinematics equation for the disk (where “C” is the contact point):

v_O = v_C + ω x r_O/C = ω x r_O/C

and solve for the angular velocity of the disk. For the acceleration problem, write down the acceleration kinematics equation for the disk:

a_O = a_C + α x r_O/C – ω²r_O/C = a_C j + α x r_O/C – ω²r_O/C

and solve for the angular acceleration of the disk.

Then, write down and use the acceleration rigid body kinematics equation relating points O and B.

Carefully study the velocity (BLUE) and acceleration (RED) information for the point on the circumference of the disk shown in the animation below. Recall that the velocity of the point on the disk in contact with the fixed upper surface is zero, and its acceleration has only a vertical component. Do you see this in the animation?

---

Any questions??