Discussion and hints:

For this problem, make your system big. In your FBD include A, B, link OA and link AB. With this choice, you can simplify your angular impulse-momentum analysis since you do not need to deal with the loads carried by OA and AB since they are internal to this system.
Step 1: FBDs
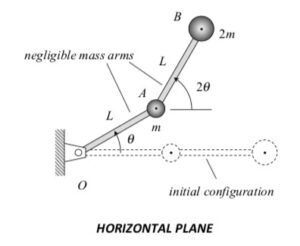
Draw an FBD of A, B, OA and AB together.
Step 2: Kinetics (angular impulse/momentum)
Consider the external forces acting on your system in your FBD. Which, if any, forces cause a moment about the fixed point O? Write down the angular momentum for each particle individually and add together to find the angular momentum for your system: HO = m rA/O x vA + 2m rB/O x vB. Is this momentum conserved?
Step 3: Kinematics
Use the rigid body velocity equation to relate the velocities of O and A. Also, use the rigid body velocity equation to relate the velocities of A and B. Note that the angular velocity of AB is twice that of OA. In the end, the velocities of A and B will be written in terms of θ_dot.
Step 4: Solve
Use your results from Steps 3 and 4 to solve forθ_dot.
Any questions?