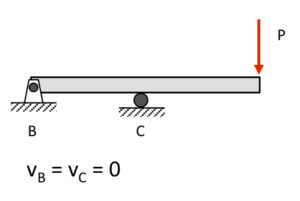
The integrations needed to determine beam deflections require the enforcement of the appropriate displacement and rotation boundary conditions (BCs). It is important that we be able to recognize these boundary conditions as we work through this analysis and be able to check our work in the end. Shown below are three beam problems and animations showing the influence of the location of the roller support condition on the shape of the beam deflection. Can you recognize how these deflection shapes are related back to the beam BCs?

 

---

Beam #1

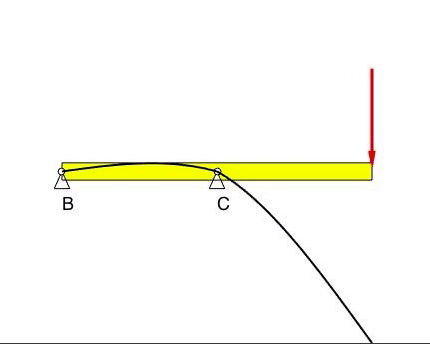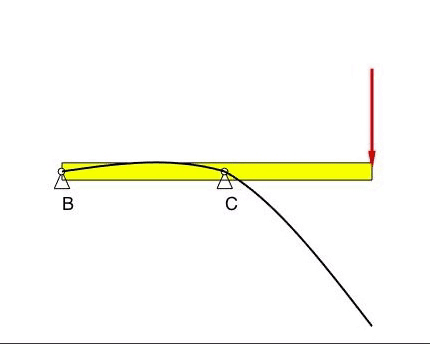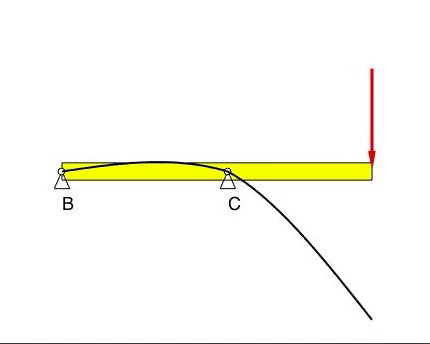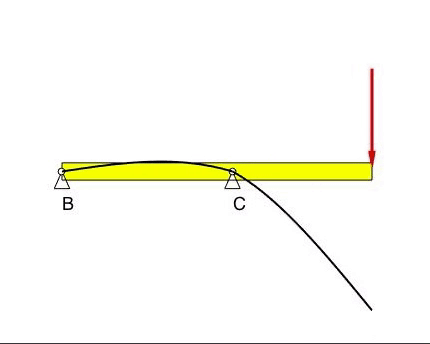
The deflection at B and C is zero, as prescribed by the BCs. There are no constraints on the slopes of the displacements at B and C.

 

---

Beam #2

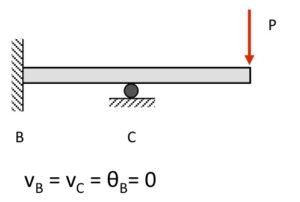
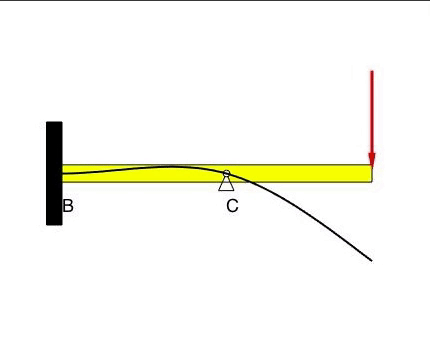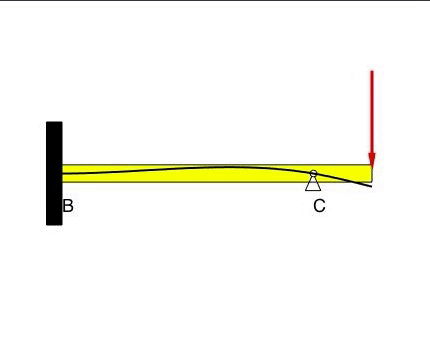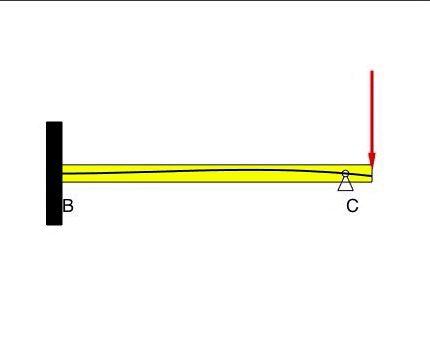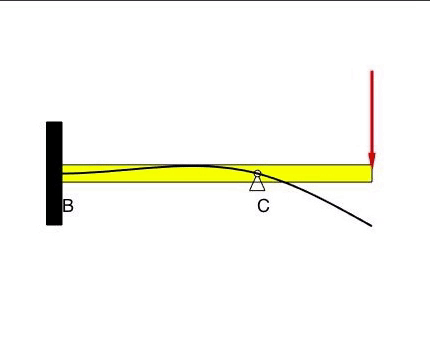
The deflection at B and C is zero, as prescribed by the BCs. With the fixed condition at B, the slope at B is also zero. There are no constraints on the slope of the displacement at C.

 

Beam #3

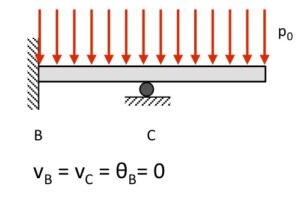
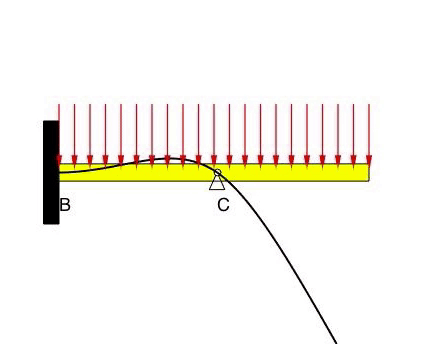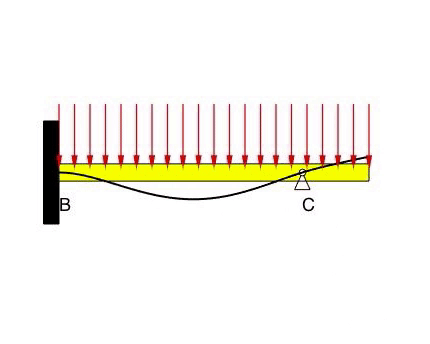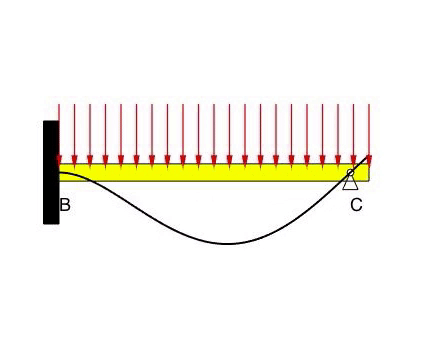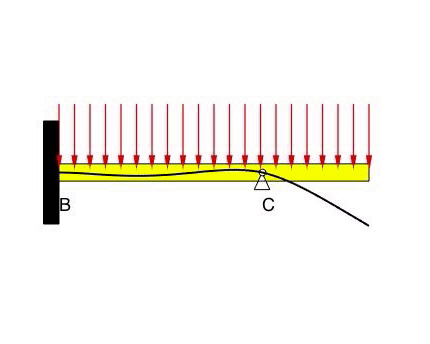
The deflection at B and C is zero, as prescribed by the BCs. With the fixed condition at B, the slope at B is also zero. There are no constraints on the slope of the displacement at C. Note that it is difficult to predict the direction (up or down) of the beam displacements due to the distributed load on the beam.