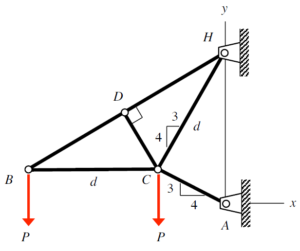
Problem statements
Solution video - H21.A
Solution video - H21.B
DISCUSSION THREAD
Please post questions here on the homework, and take time to answer questions posted by others. You can learn both ways.
Problem statements
Solution video - H21.A
Solution video - H21.B
DISCUSSION THREAD

You must be logged in to post a comment.
Should I take the moment about multiple points or treat B and C as the same moment?
I didn't take any moments, I just solved for the force equivalent in the x and y direction, from multiple joints.
I also didn't take any moments but instead I started at the joint that I had the most information about and then worked through each joint till I got the tension value for all 6 cables.
My solution did not involve taking any moments. You can set up force equivalence equations and solve for the unknowns. That will make solving it a bit simpler.
If you use the method of joints, you don't need to take a moment about any points
You only have to use Joints B,C, and D since the reaction forces are not asked for and since you can use method of joints to solve each joint one by one without running into any problems.
I did find the moments, about points A and H, in order to find the horizontal reaction forces at A and H. While this is not the only solution method, finding the horizontal reaction forces made it easier for me to find certain internal loads, like Fac.
No need to take any moments, much easier to use joint method and analyze each joint using equilibrium
You could potentially take the moment about certain points for your big initial FBD, but after that the best option when using the Method of Joints is to use the force equivalent equations in the x and y directions for each joint
When I solved this problem, I never had to take any moments. What I did instead was use the method of joints, so I was able to find the forces of each individual point. Since it is each individual point, you can't take a moment because the forces are all acting on the same point. Instead, you would use sum of forces in the x and y to find the forces of the members.
Just generally Im having a hard time seeing zero force loads is there a simple way to just look at a truss and know or no?
The easiest zero load to find would be to look at where there are "T joints" or "Y joints" with no external load applied. These are joints where 3 members come from a point, two of which are on the same axis (because they are parallel), and the third is on a different axis. In this problem, joint D would be a "T joint." In these cases it is best to think of the FBD as having the x-axis along the two parallel members. That way, when you take the sum of the forces in the y-direction, then the only force involved is the singular force not on the x-axis; therefore, this force must be zero. This works the same for a y-joint, which would be a joint that protrudes at an angle rather than perpendicular to the two parallel members. A good rule of thumb is to find these types of joints and you can immediately see that the member that is not parallel to the other two is a zero force load.
I fully agree, knowing where the zero force members are is the only way to solve this problem. Without that knowledge, you would have two many variables for the number of unique equations you can make.
The easiest way for me to identify 0 loads is if one lies on an axis and there is nothing else on that axis except for one force which just then makes it zero like a T joint where there is one force on the y or x axis alone and must be a zero load for the T joint to be in equilibrium
Is there a way to solve without the moments? And do the reactions at H and A count as part of the answer?
Yes, it is possible to solve without moment equations as you are asked to find the loads on all members of the truss which are B, D, and C. You can set up equilbrium equations in the x and the y directions for those three joints which allows you to solve for those loads and if they are compressed or under tension.
Yes believe you can solve the truss without moments using only the equilibrium at each joint, making sure that the forces in both the x and y directions sum to zero. If I am not mistaken, the reactions at A and H are the key to solving the problem, since they are part of the equilibrium system. Then after calculating you can decide if its Tension or Compression based on the answer being positive or negative. Or zero load.
You can definitely do it without using the moment; if you focus on using the x and y sums of forces on B, C, and D you can solve for the forces of the members listed as long as you keep track of your angles and consider the forces compared to the x and y axis. You can also do without reactions at A and H, because you only need the 6 equations generated about the 3 points to solve for the 6 different segments.
Why is there no Bx component in the FBD that was drawn in H21.A? The joint looks fixed, so shouldn't there be a x and y?
I'm assuming that that is because the only force that the reactions at B would be counteracting is vertical, so Bx would be equal to 0 anyways.
Yes, it is possible to solve without moment equations as you are asked to find the loads on all members of the truss which are B, D, and C. You can set up equilbrium equations in the x and the y directions for those three joints which allows you to solve for those loads and if they are compressed or under tension.
do we need to identify the reaction forces on A and H as part of the answer or just the forces on all of the truss joints?
I don't believe we need to solve the reaction forces since the problem only asks for the load carried by each member. Although the reaction forces can carry a load, they're not considered members as they are a result of the truss's interaction with the external environment, not part of the internal structure.
If the reactions at A and H are not being considered because they are not part of the truss structure, then would we need to consider the forces at A and H that act parallel to the three truss members at A and H? The reaction forces at A and H act in the x and y direction, and each have their respective moments, however do the truss forces at A and H factor into those?
To my understanding of the problem, you do not need to explicitly solve for the reaction forces as they are not considered members of the truss that we are solving. Depending on how you go about solving the problem, you may need them, but I didn't end up solving for them in my algebra.
You need to identify them as part of your FBD but not as a part of your final answer.
Depending on where you start solving it might be necessary to solve for the reaction forces at A and H and then plug them in to solve for the other forces, but the problem doesn't explicitly state that you need to solve for them and can be solved without calculating them.
No need for reaction forces just the forces on the truss joints, as the reaction forces are not counted into load/not in structure
You shouldn't have to solve for the magnitudes of the reaction forces at A and H. Just include them in your overall free body diagram.
Do you need to assume the members are in tension or compression for this problems? Also, does the direction of the P force change for tension or compression?
My professor told us to assume all members were in tension, and then if the force came out negative, we could switch it to compression. Second, the direction of P would not change as it is an external force.
Do we need to solve for the angle CBD in order to come to a final answer? I am struggling to find it with the given geometry.
I solved for the angle CBD by solving for the angle of the bigger, right-angle triangle HB(Point past C on the line between H and A) and it helped me find my final answer
I determined the angle CBD by calculating the angle of the larger right triangle HB (which is beyond point C on the line between H and A), and this led me to my final answer
To find angle CBD, take the point between HA that is aligned with line BC (lets say it's G). Then, the point BGH will make a big triangle, from there you can find angle HBG, which is the same as angle CBD.
You still are missing two of the angles, how do you get HBG without knowing GHB as well?
Nevermind, I figured it out, you need to solve for GHB using the 3-4-5 triangle given and the 90 degree angle to find one part, and then the other part is an alternate angle so it is equal to the angle found using the 3-4-5 triangle
Another correction, I am completely incorrect in this statement.
If you make a triangle of HBG, you can calculate the angle and that should lead you to the answer.
Nevermind, start by solving for the angle y axis and HC, create an imaginary right triangle still with HCG (G being imaginary point on axis), solve for angle BHG, then u can get BCD, then you can get the final angle for B
After reading through the already posted comments, why do we not consider the reaction forces at H and A? Why don't they come into play with the x and y directions of B, D, and C?
The reaction forces at A and H do not come into play for B, D, and C because they do not act at on any of those joints, Further more the force of Fca is going to be equal to the reaction force anyway. Essentially the internal forces around the triangle BCD leave no unknowns for needing the reaction forces at A and H.
Why is it that we don’t solve at point H and A for our problem? Is it because it is not our main issue to solve for?
we don't consider the points A and H because they don't affect the force between B and C. they have no force directly acting on them so they will not affect how B and C act on each other.
How do we determine whether member CD is in tension or compression given the symmetry of the truss and the loading? Would analyzing the horizontal and vertical force components at joint C be sufficient, or do we need to use method of sections to confirm the internal forces?