96 thoughts on “HOMEWORK 31 - Fall 24”

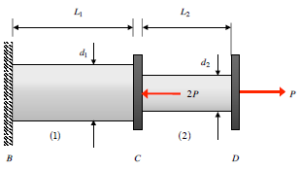
  1. Are the rods solid and the diameter refers to the distance across the cross sectional area? I’m confused because the smaller rod on the right is said to have a larger diameter. Is it just not to scale? Are d1 and d2 actually supposed to be flipped and it’s an error?

    1

    1. The rods are solid and the d1 and d2 refer to the diameters across the respective cylinders. I'm not sure if they switched the numbers or not, but I'd just do the problem using those values for their respective rods. Basically treat the sketch as completely not to scale.

      0

    4. The d1 and d2 values are referring to the diameters of the rods for the cross-sectional area. The rods are solid as well. The drawing is just not drawn to scale, but the values are correct.

    7. The rods are solid, and d1 and d2 refer to the diameters of their respective cylinders. I’d just use the given values for their respective rods and treat the sketch as not to scale.

    1. The final units for stress should be ksi. That is because it is kipps per square inch, and you are given forces in kipps and diameter in inches, which would result in square inches per area. Factor of safety, however, has no units.

    2. The final answer would have to have units as you're representing a force over an area. If there was no force the answer would just be a meaningless percentage.

    1. I think the Youngs Modulus does not have a purpose in this problem since none of the equations involve it, the only way we would need it is for the axial strain of each member which it does not ask for.

    2. I don't believe it has a purpose, since were not calculating strain, were only calculating stress which you can find from the other values given. I think, if we were only given the strain and young modulus rather than the other values we would need to use the equation for strain to back solve for the stress

    3. I think Young's modulus is sort of just there to be there, it's not necessary to solve the problem. This does look very similar to one of the lecture book questions where it asks about both stress and strain, so my thought is that this homework problem was built off of that question and that is why the Young's modulus value remains part of the problem despite it not being needed.

    5. In this problem, we do not need Young's Modulus to solve for the stress or for the factor of safety. I believe that Young's Modulus is used to calculate the strain, which can be seen from one of the in-class examples.

    2. You should consider both the 2P and the P force. This is because both would have an affect on member BC. You can ignore, though, the force of member DC, since that is an internal force. You only need to take into account external forces.

    1. For part (a), finding stress as stress= P/A gives units of kips per square inch : {kips/in^2}, which is equivalent to ksi.

      For part (b), to find FOS you’re comparing stresses in ksi, it becomes {ksi\ksi}, resulting in a dimensionless quantity, so no units are needed.

      1

  9. When calculating the normal force for member AB I got a negative answer so it is in compression so then my stress on that member would be negative, so since the factor of safety cannot be negative, did I do something wrong, or do I need to take absolute value of the stress when finding factor of safety?

    1. I think you assume that the yield strength is + for tension and - for compression. So, when you calculate the factor of safety for AB, you make the yield strength negative (since that member is in compression). The negatives would then cancel out and you'd have a positive factor of safety. I assume the yield strengths are the same for tension and compression unless otherwise stated

    2. You can neglect the sign of the normal force when calculating the factor of safety for each member because your set up for solving should be either +/+ or -/-.

  11. I got a negative stress that has a larger magnitude than the positive stress on the other part of the rod. They don't give a negative yield stress, so should I just find the FS with the positive values?

    1. I think it could mess up some of your force sum equations and moment sum equations since the directions can dictate the actual numbers too, like subtracting a number will have a different result than adding.

    2. I don't believe you have to account for the signs (tension (+) vs compression (-)) in this problem in the failure analysis. I did state whether they were in tension or compression when finding the stresses just in case but I removed the negative when calculating the factor of safety.

  13. For factor of safety, do we need one for each segment or do we account for the segment whos allowable yield strength is the least? (since this would be the maximum factor of safety for the whole rod, I assume).

    1. I believe, as you say, that the factor of safety would correspond to the part of the rod with the lowest yield strength since that would be the limiting component.

    3. I personally found both factor of safeties for both members, and labeled the factor of safety from the member with the greatest allowed yield strength as the critical factor of safety, as that is the lowest factor of safety for the rod.

    4. You can calculate the factor of safety for each segment independently then determine the overall factor of safety of the system by selecting the lower factor of safety of the two.

    2. I don't believe it matters which rod to calculate first, however, it may be easiest to work left from right to keep your work organized and minimize opportunities for mistakes.

    3. You would consider the load distribution and connectivity. Starting with rod 2 would be easier to solve first because load P is directly applied. This means you don't need to account for any load transfer. You can then go on to solve rod 1 through the connector.

    1. Yes, I found this question to be really similar to the one we did in class. I was able to solve it in a very similar manner by first finding Fn of each section and using that to find the stress. The only difference is that you have to determine if the material will fail in either section, which you can do by comparing the calculated stress to the yield strength.

  16. Some people have pointed out that the picture is not drawn to scale, that does seem to be true. Also, when solving this problem, one important thing to note is that when solving for section 1, you have to consider both forces, but when solving for section 2, you only have to consider the force to its right because if you were to take a "cut" the 2P would not affect it.

    1. The force on the right side of the rod (10 kips) does not directly act on the left section but because the two sections are connected and need to stay balanced, the left section experiences a force of 20 kips at the connection point. This force in the left section is necessary to keep the whole rod in equilibrium, even though the force does not directly cause it at the right end.

  18. Do we need to split this problem by cutting it into two separate pieces? If so could someone explain where the forces would be for the resulting two free body diagrams?

    1. No, you do not need to use Young's Modulus to solve this problem. You are correct we do not need it as the stress can be found with the other given values in the problem.

    2. You are correct, the Young's Modulus is not necessary to solve this problem. The setup may have previously been used for a problem that needed it, so it was left in.

  21. For Member 1, can the Factor of Safety be negative? I got the Fbc (bending stress) as negative instead of positive, and I'm wondering if this affects the Factor of Safety calculation.

    1. could be wrong here but I dont think the factor of safety being negative has anything wrong with it if thats what you got since the force could simply be in compression, the magnitude is what I believe matters in this case

    2. I don't believe it matters if the Factor of Safety is negative. I think it is just the absolute value of the number you get is the Factor of Safety. I could be wrong about this but I am pretty sure you just need the absolute value of your answers.

    1. The widths of members C and D don't have an impact on the results of this problem. I just used those members to help me find the forces on members 1 and 2.

    2. I believe the connectors have negligible distance. The rigid connector just serves the purpose of making sure the rod BC doesn't rotate or move. Essentially, they do not impact the process to solve this problem.

  23. Should we have two factors of safety by the end or just one? I was able to calculate one for each member but the question seems to indicate that there should be only one factor of safety.

    1. I found one factor of safety for each member, so yes I believe you'll end up with two, assuming that neither of the sections fail. You can determine this by comparing the stress you calculated to the yield stress given for each member. If the calculated stress is greater than the yield stress, then the member will fail.

    1. We did not go in too much detail over real-world example, but some simple research shows that factor of safety can be seen in many things such as bridges, buildings, aircrafts, and even elevators. In my class, the notes show that the typical factor of safety is inbetween 1 and 3 in yielding.

  25. I found a safety factor for each part, so would you end up with two as long as both sections hold up? And when you check the stress calculated with the yield stress for each member—if the calculated stress is higher, that part won’t hold up right?

    1. Yeah you would have two safety factors, one for BC and another for CD. I had both sections with no failure as the calculated stress is less than the YP stress indicated in the question. Yeah, if the calculated stress is higher, that part won't hold up.

    1. The allowable stress is given as the yield strength in the question, so you can use that value when calculating the factor of safety (FoS). To find the FoS, use the formula:

      FoS = Allowable Stress/Actual Stress

      If the FoS is greater than 1, the rod is considered safe. If it’s less than 1, the rod has failed, as it exceeds the allowable stress and can no longer handle the load safely.

      2

    2. To check if the rod has failed, you can also compare the yield strength given in the problem statement to the stress you find in each member. If the yield strength is greater than the found stressses, the member does not fail.

  28. Does Young’s modulus play any role in determining the factor of safety here? I am unsure if I should use it. I think we only compare stress against yield strength now.

    1. I did not involve Young's modulus when determining the factor of safety here, as you would only need to use Young's modulus if the problem asked for the axial strength of the members. I only used the stress from part (a) and the yield strength to find the factor of safety.

    1. I believe it would be the opposite as a Factor of Safety less than 1 means that the object would fail. And since the Stress applied on the object is less than the yield strength the object wouldn't fail. I think it is the yield strength divided by the stress you calculate and then there would only be one because if one member fails, the object as a whole fails. So you would use the greater stress you calculated leading to the lower Factor of Safety.

    2. The factor of safety ends up not having any units this comes from when you divide the allowable stress over actual stress. These are in the same units so they cancel out.

  31. To solve this problem, I first calculate the stress in each rod segment using the formula stress equals force divided by area, where force is the applied load and area is the cross-sectional area, given by area equals pi times diameter squared divided by four for diameters one and two of each segment. Then I Substituted the given values for force, diameter one, and diameter two to determine the stress in each segment. Then, I compared these stresses to the yield strength to assess if the material has failed; if the calculated stress is below the yield strength, the material is safe. Finally,I found the factor of safety by dividing the yield strength by the stress in each segment, ensuring this value is greater than one to confirm safe operation under the given load.

  33. For Member 1, I calculated the bending stress as negative, meaning compression. Can the Factor of Safety be negative in this case, or should I use the absolute value of the stress for the calculation?

Leave a Reply