Problem statements
Solution video - H32.A
Solution video - H32.B
DISCUSSION THREAD
Please post questions here on the homework, and take time to answer questions posted by others. You can learn both ways.
Problem statements
Solution video - H32.A
Solution video - H32.B
DISCUSSION THREAD

You must be logged in to post a comment.
How does the thickness of the plate influence the shear stress in this problem, and why is it essential to include this dimension in the calculation?
The thickness is used when calculating the area that the shear stress is applied over
The thickness of the plate is used to calculate the shear stress as shear stress is force applied over shear area. The shear area is the perimeter of the hole multiplied by the thickness t.
The thickness allows us to calculate the 'inner wall' on which the shear stress is applied. Because it is a square, you would find the total perimeter of the square and multiply it by the thickness to find the area on which the shear stress acts.
Including the thickness t in the calculation is essential because it determines the total sheared area that resists the punching force. A thicker plate increases the sheared area, which, in turn, reduces the shear stress for a given force P.
The thickness is used to calculate the area of the cutout and the area is used to calculate the shear stress.
You need the thickness of the plate to calculate the surface area that is being cut. Hopefully that makes sense.
Shear stress occurs over the area that, in this case, is being sheared off. This is the perimeter of the rectangle that is cut off, so the thickness is needed to find the area of the rectangular prism that is actually removed.
The thickness is essential in calculating the area of the perimeter over which the shear stress is applied. Thickness and the provided distance b are used to calculate this area.
You use it to calculate the area that the shear stress has been applied over.
You need the thickness of the plate to calculate the surface area that is being cut. You’ll need the parameter of the square to calculate this as well, hope this helps.
Thickness is required for finding the area. To find the area of the section being punched, you can use the perimeter multiplied by the thickness. Then you can solve for the shear stress.
Thickness of the plate is considered when calculating the shear stress is because in this problem we are making a hole in the plate. If this problem only needed to make an indent in the plate, the thickness would be smaller because the shear would not go through the whole plate.
The thickness is used to calculate the area of the shear. You would need to find the thickness and multiply by the perimeter
For the area in the equation shear stress = F/A, A is found by multiplying the perimeter of the cut out by the thickness of the sheet.
The thickness helps calculate the inner wall where shear stress is applied. Since it’s a square, you find the total perimeter and multiply it by the thickness to get the area for the shear stress.
For P, did you mean kips instead of ksi since forces cannot be in this unit?
I interpreted this as a distributed load over the area of the square but I am unsure if that is correct.
The punching force is per unit area, in this case it is ksi.
According to the TAs in the tutorial room, the punching force is misprinted, and it is actually meant to be in kips.
It is my understanding that P will. be in units of kips, and the shear stress will be in units of KSI, since you divide by square inches.
It should be in kips.
I was wondering the same thing. I think its a misprint.
I spoke to my professor about the units of P, and he told me that it should be a unit of force, and assuming kips would be ok.
I asked a TA about this issue and they said it was an error and should be in kips. I hope this helps!
P should be in Ksi.
yes, I talked with professor Jones and he said it was a typo
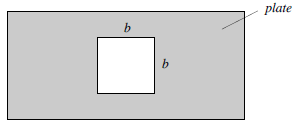
Also, I had a hard time figuring out exactly what the shear surfaces were. Can someone explain why the area wouldn't just be b*b*t?
Shear stress acts around the perimeter of the punch and extends through the thickness.
I think that is because we are dealing with shear force which acts perpendicular to the surface, like if it were "cutting", so the force only acts on the perimeter. The thickness is eventually multiplied into the formula.
Since the force doesn't act on the inside of the hole, the area is not b^2. Shear forces act on the perimeter of the sheet and through the thickness of the plate. Therefore, the area will be the perimeter multiplied by the thickness.
Shear stress acts around the perimeter of the punch not the volume, so in this case you would be using the perimeter and later multiplying it by the thickness. This is because the punch only applies the force on the surface which later leads to the actual punching which is where thickness comes into play.
The entire perimeter consists of the outer edge of the cutout. This means that you would need to multiply b*4 rather than b*b.
Sheer acts on the perimeter because that is the surface that is being torn off in this scenario. If it was a whole solid bar and we are applying a torque/ force on it THEN will we use just the area.
I think it’s because shear force acts perpendicular to the surface, like cutting, so it only applies to the perimeter. The thickness gets factored into the formula later.
The shear stress, (tau) is the shear force / Cross sectional Area. I think units would be ksi.
What does it mean when it says punching force? Is that just an overall force term?
Punching force just refers to the fact the force is creating a hole by pressing a "punch", it is functionally the same as a regular force. However be aware of the units being ksi
When they say "punching force" it is just saying the method to which they extrude the inner part, but it can be interpreted as a force we are used to.
Will shear force always be interpreted in ksi or is there a case where it is in Pa?
ksi is Kilopounds per square inch, and Pa is Newtons per square meter. Both are force divided by area, and the difference is only depending on what system you are using (metric or US customary)
I think P is supposed to be in units of kips instead of ksi. To find the shear stress you divide P by the area giving you the shear stress to be in units of ksi.
P can be in ksi, that just means you have to multiply it by the area it is acting on which is the square. Then when you solve, the square inches multiplied by ksi and the square inches in the denominator representing the area the shear stress acts on will cancel out leaving units of ksi.
Shear stress is in psi, which is pounds per square inch. Pa is just newtons per square meter, so Pa and ksi are used depending on the units presented in the problem
Is the answer supposed to be in KSI because it is a shear force? Does that mean that the punch force would be Kips instead?
If the punching force P is actually in kips (not ksi), then the answer for shear stress will indeed be in ksi after calculation. Since P should be in kips (thousands of pounds), you’ll calculate the shear stress by dividing P by the sheared area A (in square inches).
Yes I think the consensus is that there is a small typo there and the P force should be in kips.
To solve this problem, you first find the area of the hole punched by multiplying b^2 by t and then dividing P by that area. Are there more steps I am missing?
To find the area where the shear stress occurs, you would have to use the perimeter of the punch than extend through t, rather than the normal area. Shear stress occurs on the edge of the shaft for this type of question.
The perimeter of the square is what you need times the thickness for the area of the punch just like the lecture problem where it was a circular punch, circumference was used multiplied by the thickness. So it is P divided by the perimeter of the square times the thickness and that should end up in KSI.
Also, what units would the shear stress be in in this problem?
The units should be ksi. There was a misprint in the question and the P should be in kips.
Do we need a free body diagram for this problem? It seems pretty unnecessary.
I didn't bother making one since we have all of the info we need to solve the problem.
I am pretty sure that a FBD is required on homework (or at least that's what I've been told).
Towards the beginning of the semester, my professor said an FBD is always required on all homework even if it doesn't seem to be necessary. I'm sure it helps with keeping work organized and making things clear for the TAs.
I agree, even though sometimes they might not take points off for it, its just a good habit.
I think it is still needed for overall visual clarity in the problem, you can draw the arrow for the punch force and also dimension add the needed dimensions including the thickness.
I did a FBD of the area where the shear froce is applied expanded and showed P and the diretion of the shear, along with the dimensions. Im pretty sure the concpetual part of this problem they want us to show where the shear force is in the problem
I'm not sure if you need one. I drew a free-body diagram from a side view of the metal sheet to account for the thickness and shear force.
I spoke to a TA in office hours and I was told that a FBD is not necessary for this problem.
I tried to make one form a horizontal point of view just in case.
I am struggling to visualize how shear force acts "along the perimeter", can anyone explain? In the textbook, there is an example where the region being punched was circular, and the area that the shear force acted on was the circumference times the thickness. In this problem, would that translate to the area being the perimeter of the square times the thickness?
Yes, it would be the perimeter times the thickness. When we are punching the hole, you can think of the area as the metal that gets exposed by punching out the hole. That is what had to be sheared through to punch the hole out.
In this problem, the shear force acts along the perimeter of the square hole being punched. Since the hole is square with side length b, the shear area is calculated as the perimeter of the square (4b) times the thickness t. The shear stress is then found by dividing the punching force P by this shear area:
τ= P/4b*t
The shear force acts "along the perimeter" because the bonds between the molecules along that "plane" in the material are bonds that provide the reaction force against the force applied & break when there is material failure or over-stressing, causing the punched hole.
The way I think of it is that the perimeter or edges of the square is what is "holding on" to the square that is attempting to be cut out of the metal sheet so that is where the shear force acts
The way I think about it is the shear force acts along the perimeter because the molecular bonds along that plane provide the reaction force. These bonds break under overstress or material failure, causing the punched hole.
What does it mean when it says punching force?
By punching force it means that the force being applied creates a hole in the sheet of metal. So it is basically referring to the force of P.
What is another way to visualize the shear force as a result of the punching force?
The shear force is the force applied on the bonds between the molecules along that "plane" in the material (perimeter * thickness = area of stress that is parallel to the force applied) that provide the reaction force against the force applied & break when there is material failure or over-stressing, causing the punched hole.
The shear force can be visualized as being spread evenly along the edges of the hole, where the punching force cuts through the material. For a square hole, it acts along the perimeter of the hole, which is 4b, multiplied by the plate's thickness t.
Is a free body diagram necessary on this homework?
I don't think that a free body diagram is "necessary" for this problem, but you never know what they will take points off for, so it doesn't hurt to add one.
I would add a diagram that includes the measurements given in the problem that way you use everything they give you in a corresponding fbd.
I believe a free body diagram is always necessary for homework. I would recommend just drawing a simple one as this problem doesn't require a lot.
I do not believe a free body diagram is necessary for this assignment but I may be wrong
I have seen conflicting reports about P being in ksi or kips. Should I just assume its kips and solve that way?
I just assumed it was in kips because the final units would be in ksi.
You should assume that it is in kips because ksi is a unit of stress rather than force so it should be measured in kips.
I still included a FBD just to be clear, but I know it doesn't really seem necessary. Also I believe P was supposed to be in kips not ksi because ksi is the unit in the final answer.
So units for P are supposed to be in kips not ksi right? I think this may be a misprint.
P should likely be in kips rather than ksi, since ksi is a unit of stress, not force. Using kips for P will result in shear stress in ksi after dividing by the area in square inches.
What would a FBD look like on a question like this? Do you draw it from a vertical view or a horizontal view?
I would recommend drawing a top down view that clearly shows dimensions, as well as a orthogonal view to show the depth and force going vertically.
Doing one will help with visualizing the problem, it would probably since the FBDs show the metal and the location of the force.
You can use a circle with an x through it to indicate the z line coming out of the page.
This problem seems pretty straightforward, however one thing we need to note is that Shear stress is P/A, but A isn't exactly b^2 * t, it's actually perimeter * t, so 4b *t. This is just something I noticed that I was initially confused about.
I was confused about that too. There is a difference between area and the shear area. Shear area is the perimeter, or in the case of a circular cut, the circumference times the thickness, whereas normal area is the basic area calculation.
Would the final units then be in kips/in^2? Or is there another form they want the units in?
I believe that the final answer should be in kips/in^2 because the perimeter would be measured in inches squared while the force you can put it in kips so I would leave it like that.
The final answer should be in ksi, the punching force should be in kips, I believe it's a typo in the problem statement
Im pretty sure ksi is equal to kips/in^2 so I don't think it's a typo
In determining the shear stress for the punching force, how does the thickness of the plate (t) influence the result? If we increased or decreased the thickness, how would that affect the necessary punching force to maintain the same shear stress? Additionally, would a different hole shape (like circular instead of square) change how we calculate shear stress, and if so, how?
Well, for this problem the smaller the thickness the less punching force is required because there's an inverse relationship. I think it wouldn't change how you calculate the answer, just using different areas/parameters.
What units would the shear stress be in in this problem? And what should my FBDs look like?
The shear stress should be in ksi. The P force units are a typo, and should be kips, not ksi. And I do not think a FBD is required for this specific problem
As previously said, the units should be in ksi. As for the FBD, I would recommend drawing a top view FBD that clearly shows dimensions as well as an orthogonal one to show the vertical force components and thickness.
Would the given punching force P to punch out the hole in the sheet create some sort of bending moment at the points where the sheet is held up? What about if the sheet is laying on a flat surface that has a hole in it directly below where the punched out section is. Would the bending moment(s) then be on the edge of the surface cutout?
bending moments should not be necessary in this problem to my knowledge, only the forces themselves should be sufficient.
Quick tip to anyone working on the problem, the force P should be in units Kips not ksi. It is a misprint.
Is there a specific unit to use in the answer for this problem? When you do the calculations, the forces cancel out to equal kips, but I thought that was not a measure of stress.
The thickness is used to calculate the area.
What would the final units for shear stress be?
The units for sheer stress would be ksi because it is the force (kips) divided by the cross sectional area (in^2) which results in ksi.
The area used in the calculation is measured by the walls of the punched hole.
To solve this problem, I first calculated the area of the sheared surface by multiplying the perimeter of the square hole by the thickness of the plate, which is 0.1 inches. This gave me an area of 0.8 square inches. Then, I found the shear stress by dividing the punching force of 30 ksi by the area. The result was a shear stress of 37.5 ksi.
Is that the only way to figure it out or that is the simpliest way?
Whats the approach to drawing a FBD for something like this?