Problem statements
Solution video - H35.A
Solution video - H35.B
DISCUSSION THREAD
Please post questions here on the homework, and take time to answer questions posted by others. You can learn both ways.
Problem statements
Solution video - H35.A
Solution video - H35.B
DISCUSSION THREAD

You must be logged in to post a comment.
What is the real meaning behind pure bending force, I know it occurs at V=0 but why?
I think it means when there is purely (only) a bending force acting. That is why when the shear force is 0 and there is a bending force, there is a pure bending force.
When you are calculating for later segments, like 2<x<4 or 4<x<6, why do you still account for prior segments in the calculations for V and M?
What "section" should we start at? The right or the left end?
I started from the left end because that’s where the beam’s supports and loads begin. It allowed me to build the shear force and bending moment diagrams sequentially. Starting from the left also made it easier to apply equilibrium equations systematically.
It also helps to start of the left end, so that the origin is lined up with the starting point which will make the graphs make more sense when sketching them.
It is also easier to start on left as then you don't have to deal with the reactions at D.
Sorry, technically the reaction still matters for the diagrams but you know whatever the reaction is at D will just bring both diagrams back to 0 at that point so you don't actually have to calculate it.
Because the graph aligns better when working left to right, I think that it makes most sense to work from left to right. However, in order to solve the problem, you must first solve for the Moment at point D which requires starting the calculations from the left.
Calculations from the right******, sorry
You should start from the left side since that is where the forces are first placed.
I think that we should start from the left because that's where the supports and loads begin.
Unsure what they mean by the pure bending force is; can anybody help me?
Pure bending is where bending moment exists, with no other forces acting on the beam. Therefore, in this problem, the net shear force acting on the beam is zero (V = 0).
I believe pure bending force refers to where a beam only experiences a bending moment without any additional forces such as axial, sheer, or torsional forces acting on it.
What is the difference between pure bending and regular bending?
Pure bending means that there is only a bending force at the specific point. That means the shear force has to equal zero to consider a non-zero bending force a pure bending force.
Does the term pure bending have any effect on the problem? Or is it just a way to describe a specific scenario?
pure bending is where the shear force is equal to 0, so a scenario
It is also helpful since it shows where the max moment is going to be at.
Pure bending is a point on the beam where the shear force is equal to 0 so it is something common to find on these types of problems.
Is a FBD diagram necessary for this problem?
Since there's distributed loads here it's useful to turn them into individual forces occurring at points along the beam, so yes a free body diagram is necessary. FBDs are valuable to solve any statics problem - I'm also sure that graders are looking for them so I would include them as to not lose any points.
Yes, a FBD is necessary for this problem to figure out the moment and shear force equations necessary for making the coinciding graphs. The graphs are then used as a visual for where the pure bending moment occurs and what the value of moment is at that point to use in the maximum stress equation.
What's the difference between normal stress and shear stress? Are the formulas different depending on what is happening to the beam?
Nevermind...
When solving for the maximum normal stress, what should be the value for y max? Is it the diagonal of the square cross section? Or is it just one of the sides? Thanks!
The value of y max is going to be the centroid of the square cross section. So it will be the y component of the centroid (1/2 * 0.1m).
The value of y_max is the distance from the centroid of the cross section of the beam to whatever the furthest point vertically is, no matter if it is positive or a negative distance. This is because when talking about stress, you usually take into account the magnitude, not necessarily if it is negative or positive.
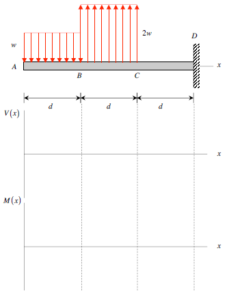
I want to check my graphs with you all, as I may have drawn incorrectly. I have gotten points off in the past so I want to double check. For V(x), I have a negative line from 0 to -20, then a positive line from -20 to 20, then a straight line to the end. For M(x), I have a negative curve from 0 to -20, then another negative curve from -20 to -30, then a positive curve from -30 to -20, then a straight line from -20 to 20. Thank you!
I have that same graph from how I interpreted it. I'm unsure of whether there is a point where there is pure bending, since pure bending exists when the shear is 0. Not sure how I would approach the maximum normal stress if there is no point where pure bending exists
There might not be a section where the shear stress is zero, but there is a point where the line crosses the x-axis, meaning at that point the shear stress is zero. You just need to find the point and use it to find the maximum normal stress.
When finding the locations at which the pure bending occurs, do I need to specify a point of which it occurs or do I just give an area like between A and B?
Since it is at a point in between I would specify where it the pure bending is in the diagram and then for your answer be specific between what two points does the pure bending occur.
When I am creating my shear force diagram, does the value from C to D equal 0 or the sum of all the forces before it?
It should be a horizontal line with the sum of the forces before it and then once it reaches point D it should go back to 0 vertically.
I am confused on what pure bending actually means or is. Is it just when the bending moment is constant by looking at the diagram or when the shear force equals zero? I just don't really understand what pure bending is.
A pure bending moment is when there are no shear forces. If you make a shear graph, the pure bending moment is where your line crosses the x-axis (y = 0).
When finding the maximum normal stress, do you use the max moment from the diagram in the stress equation. Also, is there more than one location or is there just one location of pure bending?
You can calculate stress using: normal stress = Maximum moment at the location of pure bending * distance from neutral axis / moment of inertia.
Pure bending occurs when V(x) = 0, so use the graph or calculate when shear force is = to 0.
Should the answer of the maximum normal stress be in units of KN/m^2?
The units for maximum normal stress should be in MPa.
I'm not sure which way to approach this. Should I be doing the calculations and plotting both graphs? Or plot the first graph and find the second through integration? Both are possible ways to solve correct?
Both methods should work it just depends on how you choose to solve it. You can begin with the shear force diagram and use integration to solve this or you can work out the shear and moment equations and then calculate stress separately using: normal stress = Maximum moment at the location of pure bending * distance from neutral axis / moment of inertia.
Are we supposed to use a double integral to find the second area moment of inertia.
There is no need to use double integrals in this problem. You only need the moment where there is pure bending on the beam. This can be found from looking at the shear stress graph as well as the moment graph after graphing them.
I think we are, since we need it for the max normal stress equation: max normal stress = -M*(ymax)/I, where I is the second area moment
What direction should I start from, the left or the right side? I was also confused about the units. Should we keep it in SI units of use, MPA?
I personally started by solving for the reactions at point D, and then made a shear graph and a moment graph. I started my graph from the left side to the right side. Also, yes it is my understanding that the final answer is in pascals.
There are different ways to solve this problem but I am starting with the shear force diagram and using integration to solve. Another way discussed in class is to use the shear and moment equations and then calculate stress after with the equation normal stress = max moment at pure bending location x distance from moment of inertia.