Problem statements
Solution video - H13.A
Solution video - H13.B
DISCUSSION THREAD
Please post questions here on the homework, and take time to answer questions posted by others. You can learn both ways.
HOMEWORK 13 - SP 25
11 thoughts on “HOMEWORK 13 - SP 25”
Leave a Reply
You must be logged in to post a comment.
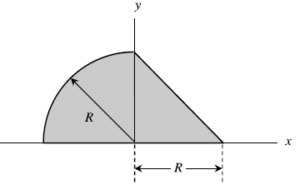
I found the quiz problem for this topic to be very helpful for this homework. The problem is relatively simple since it only includes two geometric shapes with no cut outs. The tricky part is finding the centroid for the quarter circle, and the quiz problem helps clarify how to find those values.
Are we expected to memorize certain geometric properties for the exam? For example, this problem requires us to know where the centroid of a quarter-circle is relative to its flat edge. Is this something we would be provided with on exams?
The exams do seem to have an equation sheet. But I am not sure if this exact formula will be on it. I think it is better to try and memorize it just to be on the safer side.
Since there only really exist formulas for rectangles, triangles, and circles, it can't hurt to memorize just those three (with quarter/semi-circle being a derivation of the circle)
If you have taken Calc 3, you should be able to easily derive the centroid of any simple geometric shape. The general formula for x-bar is the definite integral of x*y dx over the region where y is a function of x, then divided by the total area. For the quarter circle, convert to polar coordinates; the integrand becomes r^2cos(theta). The bounds for theta is [0, pi/2], the bounds for radius is [0, R]. This is easily computable by hand. Don't forget to divide the integration result by the area: pi * R^2 / 4.
The exams have an equation sheet, which may contain COM for geometric shapes. You should probably memorize the basic ones, like a triangle is h/3 and h/3. If there is any goofy shape, they will give the COM. I would guess a quarter circle would be given on an exam.
This problem is straightforward, and I overthink it at first. However, after actually reading it and figuring out the equations, the problem became very easy. I hope I can remember all the equations by the first exam.
all my answers are in terms of R right now, but should I have it in terms of R and pi?
I believe it says just to have answers in terms of R so I would leave them that way. It will make it easier for graders to recognize the numerical answer if you have exactly what they do so that is probably best.
4
Hello Aarav,
I left my answer in terms of R and π because I think we can treat π as a number.
I believe so, all of my answers contain pi and R. I also tried solving for the centroid via integration, and arrived at the same answer.