Problem statements
Solution video - H14.A
Solution video - H14.B
DISCUSSION THREAD
Please post questions here on the homework, and take time to answer questions posted by others. You can learn both ways.
HOMEWORK 14 - SP 25
16 thoughts on “HOMEWORK 14 - SP 25”
Leave a Reply
You must be logged in to post a comment.
I found the quiz problem from this topic to be very helpful when solving this problem. The tricky part about this problem for me was finding the bounds for integration, and the quiz problem was a good reference for it.
I second this, great advice!
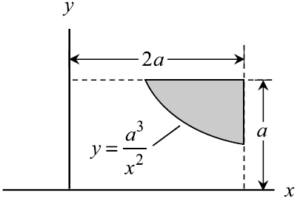
I'm unsure how to set up the integral for area. From the diagram, it looks like the x is from a to 2a, but do we know this?
You can set the the y in the equation equal to a and solve for x
you can equate y=a^3/x^2 to y=a, which is the line dotted line above, and x evaluates to a, which gives us the limits of x from a to 2a
It can be set up for y or x if you are using the double integral method
Is the right way to setup the problem to set the bounds as such?
dy = a^3 / x^2 to a
dx = a^(3/2) / y^(1/2) to 2a
Or is there a simpler way?
the examples in class required double integration because we were finding the area between two curves. I tried your wat at first, however, I think this problem can be done with a single integration since the shaded region is only bounded by one curve. you can do the area of the rectangle - the area under the curve.
I believe the x bounds go from a to 2a. For the given curve equation, if you set y = to a, you'll find that the lower curve meets the upper line at x = a.
you can take the limits of x from a to 2a, by equating a^3/x^2 to a (the dotted line above) and seeing that x evaluates to a
I have started solving using the single integration method. I was able to solve for my area using an integration along x from a to 2a. However, when I solved for my x centroid I got a natural log in my answer. This is because when I multiplied the x from the centroid equation through my lower y bound I got a^3/x. And taking the integral of this value yields a^3(lnx). I was wondering if anyone else got this value or if I made a mistake somewhere along my integration?
I also got a natural log in my integration for the x coordinate of the centroid. I would check how things cancel and review the rules for logs to see if there is a way you can reduce the natural log part to a coefficient in front of (a) to simplify the equation.
Would it be better to leave the answer in terms of ln or in terms of the actual numerical value of the ln?
numerical value, it's easier for the graders to evaluate answers
I think it would be better to give the answer as the numerical value. Basically with some decimal value in front of a.
The challenging part of this question is to find the bounds. After finding the bounds, the integration isn't that bad. I found the video of 14A helpful.