Problem statements
Solution video - H15.A
Solution video - H15.B
DISCUSSION THREAD
Please post questions here on the homework, and take time to answer questions posted by others. You can learn both ways.
HOMEWORK 15 - Sp 25
21 thoughts on “HOMEWORK 15 - Sp 25”
Leave a Reply
You must be logged in to post a comment.
I noticed that the homework problem says to leave answers in terms of pw, W, and R, at most. Do we assume the metric system for this problem and have the gravitational constant to be 9.81m/s^2?
I think so. I assumed that the gravitational constant was 9.8m/s^2. I checked my answer with a TA and it was right.
Jim Jones told me today that we could leave it in terms of g.
I think so unless the problem specifically has it in non-metric measurements I believe we should always do calculations in metric measurements.
My prof said that that was a typo, and the answer that they have has g in the answer. She said it was fine to keep g in there or multiply by 9.81.
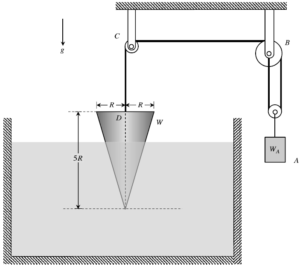
Do we assume the cone has submerged the whole depth of 5R to calculate the amount of water displaced?
Since they're asking for the minimum weight of WA, I think we have to assume it'll pretty much be completely submerged.
The minimum weight of the block can be found when the buoyant force is at its maximum, which is also when the entire cone is submerged.
I agree, since we're not given a percentage of it that is submerged, we wouldn't be able to solve if we didn't assume the cone to be completely submerged.
Do we assume the cable is splitting the tension due to block A in half, given it is attached to point B?
Since the tension is T on both sides of the pully, the force on the Block A going upward should be equal to 2T. This is what I assumed to be true.
This is also what I assumed, and my answer makes sense based on what I got.
I had the same doubt too. However, I believe that the cable does split the tension due to block A in half because one of the cables is attached to point B (which would negate half of block A's tension). So, in this case, I think you are right.
Wait, but if it splits the tension between the two cables, wouldn't it just rejoin as a tension = to the weight force, which is W?
You are correct that the tension in the one cable attached to A is just a single value of tension. However, this tension is a combination of the T pulling up on the right side of the pully and the T pulling up on the left side of the pully. Therefore, the combination of the two tensions into the one tension of the cable acting on Block A should be 2T which is then equal to the weight of Block A, W.
I believe the tension throughout the cable should be equal. This would mean that we have a force of 2T pulling up against block A.
I’m having trouble accessing the H15.B video. It says the video is private, and I was wondering if anyone had a solution or if the video setting is subject to change soon.
The problem first seems very complicated, but after looking into it, it is pretty simple. There are no complicated forces, and the free-body diagram seems simple.
The H15.B video isn't available; please fix.
The cable connecting the the cone and block is continuous which means that on the end of block A it is pulling up with double the magnitude of tension. This allows for you to solve for the tensions relationship with the weight of block A. Then, you can use the net force in the y direction while substituting in the given variables for the buoyancy force.
Should we assume that the cone is half submerged? Also, when finding the tension forces, should we write the tension for A as 2T?
You can't assume anything based on a diagram. It says the minimum before it's submerged, so I believe it means right as it would become fully submerged.