Problem statements
Solution video - H16.A
Solution video - H16.B
DISCUSSION THREAD
Please post questions here on the homework, and take time to answer questions posted by others. You can learn both ways.
HOMEWORK 16 - SP 25
12 thoughts on “HOMEWORK 16 - SP 25”
Leave a Reply
You must be logged in to post a comment.
I found the example problem from Monday's lecture to be helpful since it gives a reference for finding the force from the water. It also helps with how to find the weight of the block once the force from the water has been found.
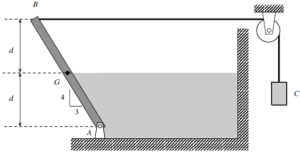
I broke up the distributed force of the water into a rectangle and a triangle, but I'm unsure of how to get the volume of the rectangle because we aren't given a length from A to the wall. Has anyone else run into this problem, or do you just use the depth of the rectangle and the dimension of the gate into the page?
When considering the force of water acting on the slanted gate, it may be helpful to partition the force into vertical and horizontal components. For the vertical component of the force, only the water directly above the gate is relevant; it's the volume of that water multiplied by the water's specific weight (rho * g). For the horizontal component, rather than trying to find the pressure distribution on the entire slanted gate, it's useful to only consider the pressure distribution acting on the gate's projection onto the vertical axes. In this case the pressure distribution is triangular; the pressure increases with depth.
Using the method I've described, you do not need to consider the gate's distance from the wall on the right.
You shouldn't have a rectangular volume. The pressure from the water has a linear relationship, so you should end up with two triangles.
I talked with my instructor today and it's possible to find the equivalent hydrostatic force without partitioning into vertical and horizontal components. Since the gate is a linearly-sloped surface, the resultant pressure distribution (vertical and horizontal combined) is still a right triangle. Multiply this pressure by the total area of the gate, you get the equivalent hydrostatic force. Using this method, it is also much easier to find the center of pressure, and its projection along the length of the gate. In fact, it's easier to find the resulting moment from the hydrostatic force with the projection, since the gate is orthogonal to the hydrostatic force.
So for this problem, you are supposed to just use the depth of the water, I believe. It also confused me because in class the day the homework was due we learned to split the water up into sections, but that was for a curved surface. This you just simply say the equivlent force is a triangle with height 5/4 d, and width 5/4 gd.
When I am drawing the free body diagram, do I split it into two separate diagrams or do I draw it as one for the pulley and the water.
I believe it can be done as one fbd as the pulley system has no friction and just acts as a horizontal force on the gate
The way I approached the problem is using the single equivalent force method. I solved for the equivalent force from the water by using it's pressure and the volume of the triangular prism it creates. Then you need to solve for the equivalent point of application which is a third up from the base of the triangle of the water pressure. To solve for the weight of C, I summed the moments about point A which reduces the amount of unknown variables.
Page 178 has a helpful example for understanding the forces on a surface at an angle.
I also used moment about A to solve for the weight using the forces of water weight, they hydrostatic load, and the tension force of the cable. The solved example problem (5.E.3) on page 183 of the lecture book is a handy reference.
What kind of force does water exert on the gate?