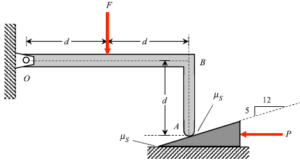
Problem statements
Solution video – H20.A
Solution video – H20.B
DISCUSSION THREAD
Please post questions here on the homework, and take time to answer questions posted by others. You can learn both ways.
HOMEWORK 20 – SP 25
14 thoughts on “HOMEWORK 20 – SP 25”
Comments are closed.
If I am not mistaken the force of friction would point to the right correct? I think this is the case because the force P and the force are both pushing to the left so the counteract this force wouldnt friction have to go to the left?
The force P is pushing to the left. If you are solving for the force P required to move the wedge to the left, the friction would point to the right. The friction should point in the opposite direction of the impending motion you are solving for.
The force P is pushing to the left. You are solving for the force P required to move the wedge to the left, so the friction would point to the right. (You want the largest P, so you would want the situation where you move it to the left). The friction should point in the opposite direction of the impending motion you are solving for.
Point O is a pin and not a fixed support right? I just want to make sure I set up my reactions correctly.
The question says that the the arm is pinned to the ground at O. So I think they do mean that it is a pin support.
Hello,
I was wondering, will the frictional force when the L-shaped object is pushed down become larger if the impending motion of the system is when P pushes the L-shaped object upwards on its slope? In comparison to when the L-shaped object is pushed downward by the force F?
I believe when the L-shaped bar is pushed down, it increases the force on the block and hence the reaction force leading to increased friction. I believe P is already pushing the L-bar “up” in a sense that its impending motion is a counter-clockwise rotation.
If anyone likes to work with an example nearby, I found example 6.E.2 in the lecture book helpful for this problem.
Does impeding slipping apply here and if so do we need to draw a separate free body diagram for it?
Do we need to determine the P when the impending motion get switched to the right?
You must consider both situations of impending motion, solve for P, and take the value that causes the system to remain in equilibrium.
However, since we are looking for the largest P value to keep the system in equilibrium, it can be assumed that this will be the case where the impending motion is to the left, so both situations aren’t completely necessary.
If the wedge’s and arm’s masses are negligible, wouldn’t that mean that there is no normal force?
No that is not true. Since the normal force is a contact force, and there is a force F applied to the arm, there must be a normal force present. This force affects the wedge and is necessary for the calculation.