Problem statements
Solution video – H25.A
Solution video – H25.B
DISCUSSION THREAD
Please post questions here on the homework, and take time to answer questions posted by others. You can learn both ways.
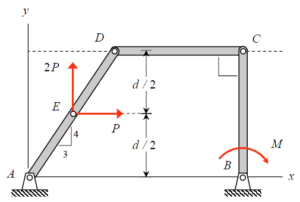
Problem statements
Solution video – H25.A
Solution video – H25.B
DISCUSSION THREAD

Comments are closed.
Although I began solving this problem by writing three equilibrium equations for each member, by the end I found that nine equilibrium equations were unnecessary. A good method to solve this problem is to work backwards, starting with the equilibrium equation containing M and then only writing equilibrium equations containing the needed series of unknowns.
I said that member CD was a two force member and solved the problem by working from the rightmost member to the left. On each member I summed the moments about points to find the relevant equations I needed to solve for the couple M required to keep the system in equilibrium.
You could solve this problem by writing out all of the equilibrium equations but it brings in extra steps which take more times. I also backtracked through the problem in order to find what exactly I needed to solve for, and thats how I created my equations which helped me isolate variables and find the solution.
I found the most important thing for solving this problem was understanding the FBD of the two-force member. Remembering that a two-force member does not experience a moment based on its applied forces is key to simplifying this problem. After doing so I found the solution process could be done within two moment equations and one force summation.
Would the best way to do this be finding the moment about about A and about point D?
Do we have to account for the angle between E and the forces on it when doing calculations?
I might be wrong, but I think as long as you maintain the normal x and y axes for your sum of forces, you shouldn’t have to do anything with angles (since all the forces are already broken up into the normal x and y directions).
When doing this problem I found that all forces are either completely vertical or completely horizontal, so I don’t believe and work with angles are necessary for this problem.
I agree, I was skeptical of this problem as well because I was confused on whether or not I should consider the angles or not. However, I noticed that I didn’t need to use it at all since all the forces are all either horizontal or vertical.
The only thing is you will have to use trig to find the distance between A and the y direction force at E if you find moment at A.
I found this problem similar to the examples we did in class. Breaking up the machine into links and assessing internal forces of each link is a good understanding of how the machine is maintaining static equilibrium even with external forces and moments being applied. Understanding the definition of a two-force member and how they work is also important in simplifying down this problem!
As other students have said prior, a good way to solve this problem is by only using moments. By analyzing member AD and DC individually, as well as ensuring you know that DC is a two force member, the problem becomes a lot easier to solve. I wonder how this problem would have been in terms of difficulty if DC was not a two force member.
I think the most helpful thing for me was identifying that DC is a two‐force member carrying no moment and then working backwards from right to left. I chose points to sum the moments around – usually it was helpful to do it at the pivot where we want to eliminate reaction forces. I was able to zero in on the unknown couple M and I didn’t have to do all the equilibrium equations.
You will be able to do this problem by writing all the forces on the FBD, and then using the equilibrium to solve for the unknown force. I think the most challenging part is the sign of the moment, because when writing the equation for the equilibrium at C. I think separating two parts, CD and AD will make it easier to solve the problem. Also, the CD is a two-member force.
Solving for general static equilibrium is generally simple but executing for the final moment is rather difficult